Cevians And Semicircles
Problem
In $\Delta ABC$ $AA',$ $BB',$ and $CC'$ are concurrent cevians. Form semicircles on $AC',$ $BC',$ and so on, externally to $\Delta ABC.$ Draw common external tangents to each pair of the semicircles on the same side of the triangle. Consider inscribed angles defined by the diameters and the chords from the vertices of the triangle to the points of tangency, as shown:
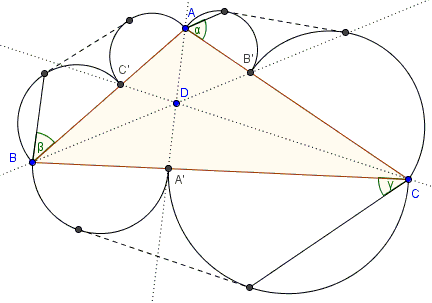
Prove that
$\tan\alpha\cdot\tan\beta\cdot\tan\gamma = 1.$
Hint
The diagram above shows only one chord of one semicircle per side. Draw a few more segments that could be relevant to the construction.
Solution
Consider the pair of the semicircles on side $AC.$ Let $P$ and $Q$ be their centers and $F$ and $G$ the points of tangency.
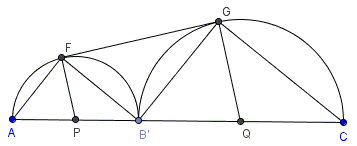
$PF\parallel QG$ because both are perpendicular to $FG.$ Therefore, $\angle APF=\angle B'QG.$ Since both triangles $APF$ and $B'QG$ are isosceles and their apex angles are equal, the two triangle are similar, implying $\alpha=\angle PAF=\angle QB'G$ so that two right triangles $AB'F$ and $B'CG$ are similar. In addition, $\Delta FGB'$ is similar to the two. This is because $B'F\perp B'G$ and $\angle B'AF=\angle B'FG.$ (The latter since inscribed $\angle B'AF$ is subtended by the arc $B'F$ whereas $\angle B'FG$ is formed by a tangent and a chord subtending the same arc. It follows that
$\displaystyle\frac{B'C}{AB'}=\frac{B'G}{AF}.$
But, from $\Delta FGB',$ $\displaystyle B'G = B'F\cdot\tan\alpha,$ and, from $\Delta AB'F,$ $AF=B'F/\tan\alpha.$ Finally,
$\displaystyle\frac{B'C}{AB'}=\frac{B'G}{AF}=\tan^{2}\alpha.$
All that remains is to apply the same considerations to the other two pairs of the semicircles and refer to Ceva's theorem
$\displaystyle\frac{B'C}{AB'}\cdot\frac{AC'}{BC'}\cdot\frac{BA'}{CA'}=1.$
This gives
$\tan^{2}\alpha\cdot\tan^{2}\beta\cdot\tan^{2}\gamma=1,$
and, since, all three angles are acute, the three tangents are positive such that taking square root is safe and yields the required equality
$\tan\alpha\cdot\tan\beta\cdot\tan\gamma=1.$
Acknowledgment
The problem has been discovered by Emmanuel Antonio José García and posted at the CutTheKnotMath facebook page.
Trigonometry
- What Is Trigonometry?
- Addition and Subtraction Formulas for Sine and Cosine
- The Law of Cosines (Cosine Rule)
- Cosine of 36 degrees
- Tangent of 22.5o - Proof Wthout Words
- Sine and Cosine of 15 Degrees Angle
- Sine, Cosine, and Ptolemy's Theorem
- arctan(1) + arctan(2) + arctan(3) = π
- Trigonometry by Watching
- arctan(1/2) + arctan(1/3) = arctan(1)
- Morley's Miracle
- Napoleon's Theorem
- A Trigonometric Solution to a Difficult Sangaku Problem
- Trigonometric Form of Complex Numbers
- Derivatives of Sine and Cosine
- ΔABC is right iff sin²A + sin²B + sin²C = 2
- Advanced Identities
- Hunting Right Angles
- Point on Bisector in Right Angle
- Trigonometric Identities with Arctangents
- The Concurrency of the Altitudes in a Triangle - Trigonometric Proof
- Butterfly Trigonometry
- Binet's Formula with Cosines
- Another Face and Proof of a Trigonometric Identity
- cos/sin inequality
- On the Intersection of kx and |sin(x)|
- Cevians And Semicircles
- Double and Half Angle Formulas
- A Nice Trig Formula
- Another Golden Ratio in Semicircle
- Leo Giugiuc's Trigonometric Lemma
- Another Property of Points on Incircle
- Much from Little
- The Law of Cosines and the Law of Sines Are Equivalent
- Wonderful Trigonometry In Equilateral Triangle
- A Trigonometric Observation in Right Triangle
- A Quick Proof of cos(pi/7)cos(2.pi/7)cos(3.pi/7)=1/8
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73593304
