Wonderful Trigonometry In Equilateral Triangle
What Is This About?
Source

Problem
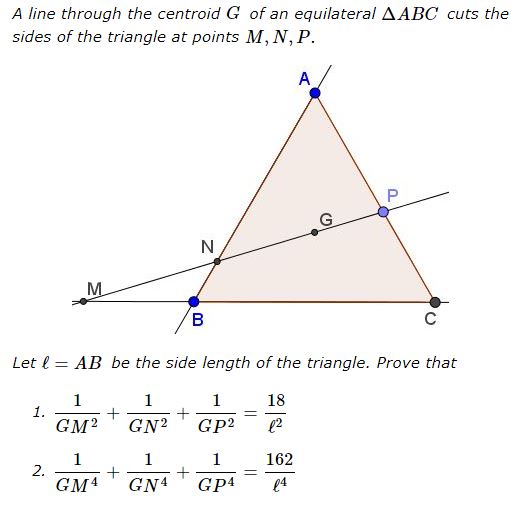
Solution 1
Let $E\,$ be the midpoint of the base $BC.\,$ Then $\displaystyle AG=\frac{\sqrt{3}}{3}\ell\,$ and $\displaystyle EG=\frac{\sqrt{3}}{6}\ell.\,$ Let $x=\angle CMN,\,$ as shown bellow. (Slight modifications will need to be made for the case where $M\,$ is on the side $BC.\,$) We shall consider triangles $EGM,\,$ $AGN,\,$ and $AGP.$
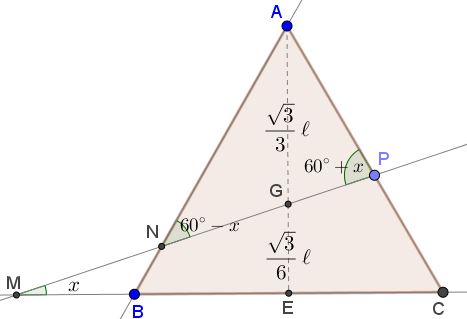
$\Delta EGM\,$ is right so $\displaystyle GM=\frac{EG}{\sin x}=\frac{\sqrt{3}\ell}{6\sin x}.$
In $\Delta AGN,\,$ $\angle GAN=30^{\circ}\,$ and, by straightforward angle chasing, $\angle ANG=60^{\circ}-x.\,$ According to the Law of Sines,
$\displaystyle GN=AG\cdot\frac{\sin 30^{\circ}}{\sin (60^{\circ}-x)}=\frac{\sqrt{3}\ell}{6\sin (60^{\circ}-x)}.$
Similarly, in $\Delta AGP,\,$
$\displaystyle GP=AG\cdot\frac{\sin 30^{\circ}}{\sin (60^{\circ}+x)}=\frac{\sqrt{3}\ell}{6\sin (60^{\circ}+x)}.$
For the first problem then we have to prove that
$\displaystyle\begin{align}18&=\frac{\ell^2}{GM^2}+\frac{\ell^2}{GN^2}+\frac{\ell^2}{GP^2}\\ &=\left(\frac{6}{\sqrt{3}}\right)^2\left(\sin^2x+\sin^2(60^{\circ}-x)+\sin^2(60^{\circ}+x)\right), \end{align}$
i.e.,
$\displaystyle \sin^2x+\sin^2(60^{\circ}-x)+\sin^2(60^{\circ}+x)=\frac{3}{2}.$
To accomplish the feat, note that
$\displaystyle\begin{align} \sin^2(60^{\circ}\pm x)&=(\sin 60^{\circ}\cos x\pm\cos 60^{\circ}\sin x)^2\\ &=\left(\frac{\sqrt{3}}{2}\right)^2\cos^2x+\left(\frac{1}{2}\right)^2\sin^2x\pm 2\frac{\sqrt{3}}{2}\cdot\frac{1}{2}\sin x\cos x, \end{align}$
so that
$\displaystyle\begin{align} \sin^2x+\sin^2(60^{\circ}-x)+\sin^2(60^{\circ}+x)&=\sin^2x+2\left(\frac{3}{4}\cos^2x+\frac{1}{4}\sin^2x\right)\\ &=\frac{3}{2}(\cos^2x+\sin^2x)=\frac{3}{2}. \end{align}$
In a similar manner, for the second part, suffice it to show that
$\displaystyle \sin^4x+\sin^4(60^{\circ}-x)+\sin^4(60^{\circ}+x)=\frac{9}{8}.$
From above,
$\displaystyle\begin{align} \sin^4(60^{\circ}\pm x)&=\left(\frac{1}{2}\cos^2x+\frac{1}{4}\pm\frac{\sqrt{3}}{4}\sin2x\right)^2\\ \end{align}$
It follows that
$\displaystyle \begin{align} &\sin^4(60^{\circ}- x)+\sin^4(60^{\circ}+ x) = \frac{1}{8}(2\cos^2x+1)^2+\frac{3}{8}\sin^22x\\ &\qquad\qquad\qquad= \frac{1}{8}(\cos 2x+2)^2+\frac{3}{8}\sin^22x\\ &\qquad\qquad\qquad=\frac{1}{8}(\cos^22x+\sin^22x)+\frac{1}{2}\cos 2x+\frac{1}{2}+\frac{1}{4}\sin^22x\\ &\qquad\qquad\qquad=\frac{5}{8}+\frac{1}{2}\cos 2x+\frac{1}{4}\sin^22x. \end{align}$
On the other hand,
$\displaystyle \begin{align} \sin^4x &= (1-\cos^2x)^2=\left(\frac{1-\cos 2x}{2}\right)^2\\ &=\frac{1}{4}-\frac{1}{2}\cos 2x+\frac{1}{4}\cos^22x. \end{align}$
Summing up:
$\displaystyle\begin{align} &\sin^4x+\sin^4(60^{\circ}-x)+\sin^4(60^{\circ}+x)\\ &=\left(\frac{1}{4}-\frac{1}{2}\cos 2x+\frac{1}{4}\cos^22x\right)+\left(\frac{5}{8}+\frac{1}{2}\cos 2x+\frac{1}{4}\sin^22x\right)\\ &=\frac{1}{4}+\frac{5}{8}+\frac{1}{4}=\frac{9}{8}. \end{align}$
Solution 2
Let $\angle BMG=\phi$. $\angle ANG=\angle BNM = 60-\phi$ and $\angle CPG=120-\phi$.
The distance of the centroid from any side is $d=l/2\sqrt{3}$.
Thus,
$\displaystyle\begin{align} GP&=\frac{d}{\sin \angle CPG}=\frac{d}{\sin(120-\phi)}=\frac{l}{2\sqrt{3}\sin(120-\phi)} \\ GN&=\frac{d}{\sin \angle ANG}=\frac{d}{\sin(60-\phi)}=\frac{l}{2\sqrt{3}\sin(60-\phi)} \\ GM&=\frac{d}{\sin \angle BMG}=\frac{d}{\sin\phi}=\frac{l}{2\sqrt{3}\sin\phi} \end{align}$
$\displaystyle\begin{align} &\sin^2\phi+\sin^2(60-\phi)+\sin^2(120-\phi) \\ &\qquad\qquad=\sin^2\phi+\left(\frac{\sqrt{3}}{2}\cos\phi-\frac{1}{2}\sin\phi\right)^2 +\left(\frac{\sqrt{3}}{2}\cos\phi+\frac{1}{2}\sin\phi\right)^2 \\ &\qquad\qquad=\sin^2\phi+2\left(\frac{3}{4}\cos^2\phi+\frac{1}{4}\sin^2\phi\right)=\frac{3}{2} \end{align}$
$\displaystyle\begin{align} &\sin^4\phi+\sin^4(60-\phi)+\sin^4(120-\phi) \\ &\qquad\qquad=\sin^4\phi+\left(\frac{\sqrt{3}}{2}\cos\phi-\frac{1}{2}\sin\phi\right)^4+\left(\frac{\sqrt{3}}{2}\cos\phi+\frac{1}{2}\sin\phi\right)^4 \\ &\qquad\qquad=\sin^4\phi+2\left(\frac{9}{16}\cos^4\phi+\frac{9}{8}\cos^2\phi\sin^2\phi+\frac{1}{16}\sin^4\phi\right) \\ &\qquad\qquad=\frac{9}{8}\left(\cos^2\phi +\sin^2\phi\right)^2 = \frac{9}{8} \end{align}$
$\displaystyle\begin{align} \frac{1}{GM^2}+\frac{1}{GN^2}+\frac{1}{GP^2}&=12\left[\frac{\sin^2\phi+\sin^2(60-\phi)+\sin^2(120-\phi)}{l^2}\right]=\frac{18}{l^2}\\ \frac{1}{GM^4}+\frac{1}{GN^4}+\frac{1}{GP^4}&=144\left[\frac{\sin^4\phi+\sin^4(60-\phi)+\sin^4(120-\phi)}{l^4}\right]=\frac{162}{l^4} \end{align}$
Acknowledgment
This surprising problem has been kindly pointed out to me by Leo Giugiuc. The problem by Miguel Ochoa Sanchez was originally posted at the Peru Geometrico facebook group and appeared on my timeline. The solution is by Aris Setiawan; Solution 2 is by Amit Itagi.
It would be exciting to find a synthetic solution to the problem, although I doubt that such one exists.
![]()
|Contact| |Up| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73564955
