Hunting Right Angles

Have you tried to form a right triangle with vertices on a square grid? It is easy of course to find Pythagorean triangles with horizontal and vertical legs. Can you find less trivial configurations? The applet below is intended to assist you with this task.

This applet requires Sun's Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun's website at https://www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet.

What if applet does not run?

If you want to approach the task of finding right triangles systematically, start with forming isosceles ones. There is a multitude of isosceles right triangles, e.g.,

Choose a point - C in the example - and a vector (u, v) - (2, 5) above. From C, first in the direction of (u, v) and then in the direction (v, -u) find points A and B. For any choice of u and v the result is a right isosceles triangle. Further examples can be found by extending one of the legs of an already found triangle to an integer multiple of its length. For example, if A is constructed as above but B is located at the end of vector 2(v, -u) that begins at C, the resulting triangle is still right.

Leg BC, in this case, passes through one additional grid point. (You may try your hand in finding grid right triangles with the help of the applet.)

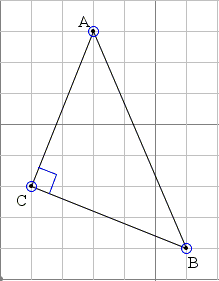
An examination of the right triangles on a square grid leads to some trigonometric identities. For example, observe that, by construction, the right angle below is the sum of two angles, one with the tangent equal to 2/5 and the other 5/2:

Thus we may conclude that arctan(2/5) + arctan(5/2) = 90°. (arctan is the inverse of the tangent. If a = tan(α) then arctan(a) = α, although the situation is a little more complex because tangent is a periodic function. Another symbol, tan^-1, is also in frequent use.) More generally,

arctan(a) + arctan(1/a) = 90°,

for any a. Additional trigonometric identities emerge from considering the acute angles. In the example above, angle A (= 45°) is split into two angles, one with tangent 2/5, the other 3/7, implying that

arctan(2/5) + arctan(3/7) = 45° (= arctan(1).)

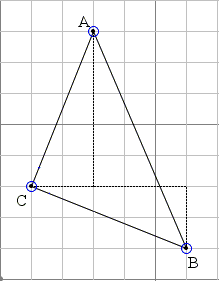
Another curious identity arctan(1/2) + arctan(1/3) = arctan(1) is illustrated by the diagram below

Here are further examples where, as before, we focus on the angle at A. The idea is that the triangles are constructed by extending one of the legs of a right isosceles triangle.

			Leg AC was extend by the factor of 2, leading to arcttan(1/3) + arctan(1/7) = arctan(1/2),
			Leg BC was extended by the factor of 4, leading to arctan(2) + arctan(2/9) = arctan(4),
			Leg BC was extended also by the factor of 4, leading to arctan(3) + arctan(1/13) = arctan(4).

In the latter one, looking at the angles at vertex B, leads to a modification:

arctan(1/4) + arctan(1/13) = arctan(1/3).

The number of such identities that, at first sight, might appear surprising is endless. Here is another one: arctan(1/4) + arctan(5/14) = arctan(2/3). R. Vakil mentions one general formula:

arctan

a - b

arctan

a² - ab + 1

for positive a and b, a > b.

Since cot(x) = tan(90° - x), all the identities we just found can be rewritten in terms of cotangent.

References

R. Vakil, A Mathematical Mosaic, Brendan Kelly Publishing, 2008 (Expanded Edition), p. 96

Trigonometry

71927536