| Manifesto | Bookstore | Contents | Amazon store | Term index | What changed? | Contact | Recommend |
Inscribed and Central Angles in a Circle: What is this about?
|
| Buy this applet What if applet does not run? |
Copyright © 1996-2009 Alexander Bogomolny
Inscribed and Central Angles in a Circle
Two chords in a circle, say AC and AB, with a common point A, define an angle BAC. An angle, like BAC, whose vertex lies on a circle is said to be inscribed into the circle. The sides AB and AC of an inscribed angle BAC cut the circle into two arcs: one that contains A and the other that does not. The latter subtends the angle BAC. (As often, it is said that the angle subtends the arc, or the chord BC.)
The arc also subtends a central angle BOC, where O is the center of the circle. The two angles, the inscribed angle BAC and the central angle BOC, stand in a simple relationship expressed by the following
Theorem
BOC = 2BAC.
(This is Proposition III.20 from Euclid's Elements.)
Proof
| Buy this applet What if applet does not run? |
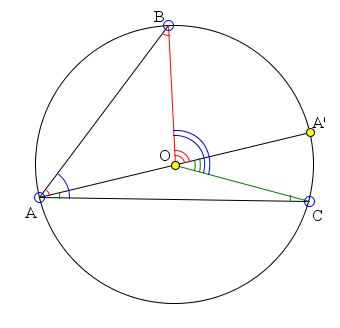
Let A' be the point on the circle opposite point A. The proof is simplest when one of the points - B or C - coincides with A'. In this case, the inscribed angle BAC is one of the two base angles in an isosceles triangle AOC. In this case, the central angle BOC plays the role of the external angle of the triangle, such that it equals the sum of the two base angles of the triangle. Since the two are equal, the proof is complete in this case.
Two additional cases have to be considered: A' may lie on either the arc subtending the inscribed angle or the one that also contains the point A. Now we'll have to consider two isosceles triangles, AOB and AOC, and the associated central angles A'OB and A'OC. Depending on the location of A' with respect to the subtending arc BC, the angle BAC is either the sum or the difference of angles A'AB and A'AC. The corresponding central angles will stand in exactly the same relationship. BOC is either the sum or the difference of A'OB and A'OC. Which reduces the problem to the previous case and completes the proof.
In a limiting case where one of the points - B or C - coincides with A, we should consider the angle between the tangent at A and the only present chord. This angle is still equal to one half of the central angle subtended by the chord. (Make the applet help you with this case.)
The relationship between the arcs and inscribed angles that we have described underscores a simple fact that circular arcs are two arcs of two circles loci of points
from a segment is seen under a fixed angle. We are forced to talk here about circular arcs and not entire circles because a chord other that a diameter of a circle divides the circle into two unequal arcs. Depending on which of the arcs the chord is being observed from the angle of observation changes to its supplementary. In particular, we arrive at the fact that opposite angles in an inscribed (cyclic) quadrilateral add up to 180o. (A dynamic illustration combines the two situations into a single framework.)
Copyright © 1996-2009 Alexander Bogomolny
| 34221419 |  |
