A Problem in Three Squares

An interesting fact holds in a configuration of three equal squares placed side by side. If the lines drawn as shown then $\angle BDC + \angle BFC = \angle BEC.\,$ There are many proofs of this result. These are so simple, the problem has been included in many a puzzle book.

First note that $\angle BEC = 45^{\circ}.\,$ The task is then to show that $\angle BDC + \angle BFC = 45^{\circ}.\,$ Let's introduce $\alpha = \angle BDC\,$ and $\beta = \angle BFC.\,$ We are to prove that $\alpha + \beta = 45^{\circ}.\,$

Add another row of squares below the given three. $\Delta BKD\,$ is isosceles $(BK = DK)\,$ and, in addition, $\angle K = 90^{\circ}.\,$ Therefore, $\angle BDK = 45^{\circ}.\,$ However, since triangles $DEK\,$ and $FCB\,$ are equal, we also have $\angle KDE = \beta .$

Now with some trigonometry $(\arctan = \tan^{-1}),$

$\displaystyle \begin{align} \alpha + \beta &= \arctan(\frac{1}{3}) + \arctan(\frac{1}{2})\\ &= \arctan((\frac{1}{3} + \frac{1}{2})/(1 - \frac{1}{3}\cdot \frac{1}{2}))\\ &= \arctan(1). \end{align}$

where I used the standard formula for the tangent of a sum

$\displaystyle \tan(\alpha + \beta ) = \frac{\tan\alpha + \tan\beta}{1 - \tan\alpha\cdot \tan\beta}.$

Since $\arctan(1) = 45^{\circ},\,$ $\alpha + \beta = 45^{\circ}.$

Triangles $BDE\,$ and $FEB\,$ are similar.

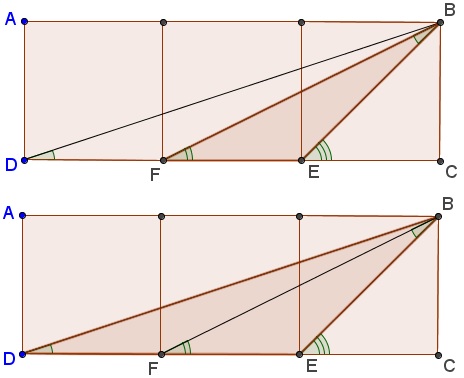
Indeed, assuming the side of the square equals $1,\,$ then

$\displaystyle \begin{array}{lll} \,DE=2, & BE=\sqrt{2}, &\displaystyle \frac{DE}{BE}=\sqrt{2},\\ BE=\sqrt{2}, & EF=1, &\displaystyle \frac{BE}{EF}=\sqrt{2},\\ BD=\sqrt{10}, & BF=\sqrt{5}, &\displaystyle \frac{BD}{BF}=\sqrt{2}. \end{array}$

which implies that $\angle BDC = \angle FBE = \alpha.\,$ Finally, the exterior angle $BEC\,$ of $\Delta FEB,\,$ equals the sum of the opposite interior angles, i.e., $\alpha + \beta.\,$ In short, we proved that

$\displaystyle \arctan(\frac{1}{2}) + \arctan(\frac{1}{3}) = \arctan(1).$

Observe that this implies another identity:

$\displaystyle \arctan(1) + \arctan(\frac{1}{2}) + \arctan(\frac{1}{3}) = \frac{\pi}{2}.$

Following a proof without words by Hasan Unal (Math Magazine, v 82, n 1, February 2009 , p. 56) we shall prove a more general statement. Let x and y be positive numbers satisfying $x^{2} + y^{2} = 1.\,$ Then

$\displaystyle\arctan\frac{1-x}{y}+\arctan\frac{1-y}{x}=\frac{\pi}{4}.$

The identity $\displaystyle \arctan(\frac{1}{2}) + \arctan(\frac{1}{3}) = \arctan(1) is obtained from the above by letting $\displaystyle x = \frac{3}{5}\,$ and $\displaystyle y = \frac4}{5},\,$ making it yet another appearance of the Egyptian 3-4-5 triangle. The proof is based on the following diagram.

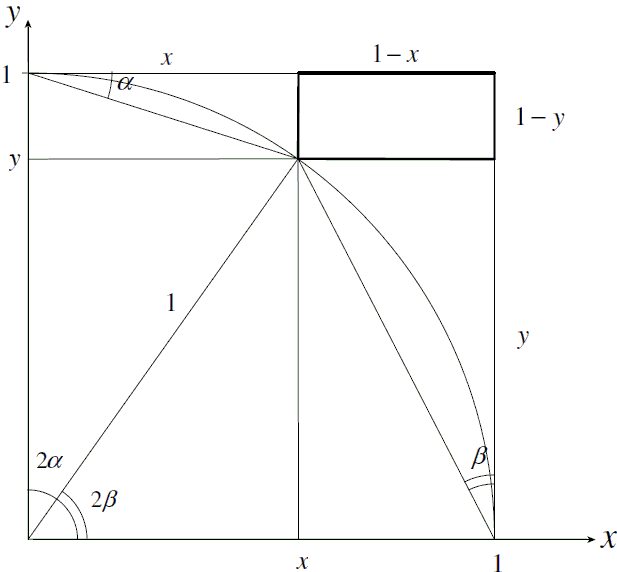
Set $\displaystyle \alpha = \frac{1 - y}{x},\,$ and $\displaystyle \beta = \frac{1 - x}{y}.\,$ We see at the origin that $\displaystyle 2\alpha + 2\beta = \frac{\pi}{2},\,$ implying $\displaystyle \alpha + \beta = \frac{\pi}{4} = \arctan(1).\,$

Elsewhere we prove another curiosity: $\arctan(1) + \arctan(2) + \arctan(3) = \pi.$

This and the next proof are from David Wells' newsletter, where more accurate references can be found.

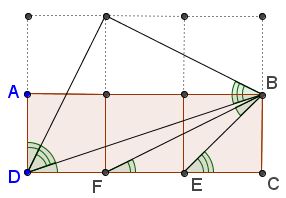
This is a variant of proof #1 that qualifies as a proof without words.

The extra construction here is the circle circumscribing a five-square cross.

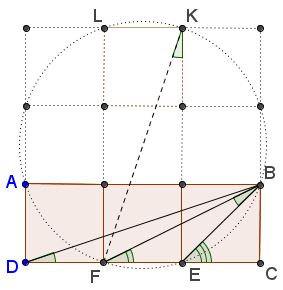
Here we have $\angle CDB=\angle EKF=\angle EBF,\;$ (as inscribed subtended by the same arc.) In addition, by the Exterior Angle Theorem, $\angle EBC=\angle EBF+\angle BFE.$

1. B. Richardson, Three Squares Theorem, in The Changing Shape of Geometry, edited by C. Pritchard, Cambridge University Press, 2003
2. A Decade of the Berkeley Mathematical Circle, The American Experience, Volume I, Z. Stankova, Tom Rike (eds), AMS/MSRI, 2008
3. A Decade of the Berkeley Mathematical Circle, The American Experience, Volume II, Z. Stankova, Tom Rike (eds), AMS/MSRI, 2015, pp. 173-174
4. D. Wells, Archimedes Mathematics Education Newsletter, #3, September 05 2016

The identity $\arctan(1)+\arctan(2)+\arctan(3)=\pi\,$ can be derived by paper folding and also becomes obvious in the 3-4-5 (Egyptian) triangle.