Sine of the Sum Formula

The applet below illustrates a proof without words of the "sine of the sum" formula due to Volker Priebe and Edgar A. Ramos [Nelsen, p. 40].

---

This applet requires Sun's Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun's website at http://www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet.

---

The rhombus inscribed into a rectangle has side length of 1. The rhombus cuts off of the rectangle two pairs of equal right triangles. The acute angles of the triangles are A, 90° - A, B, 90° - B. The vertices of the rhombus split the sides of the rectangle into segments of lengths cos A, sin A, cos B, sin B, as shown.

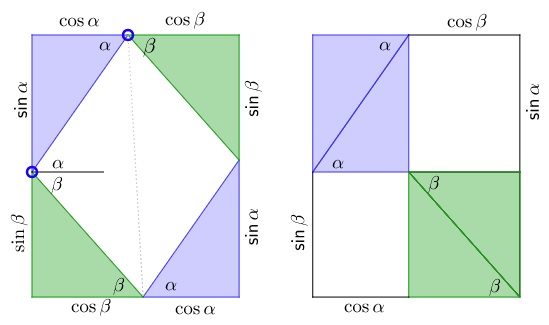
The area of the rhombus is sin(A + B). In the right half of the applet, the triangles rearranged leaving two rectangles unoccupied. The area of one is sin A × cos B, that of the other cos A × sin B, proving the "sine of the sum" formula

sin(A + B) = sinA cosB + cosA sinB.

References

1. R. B. Nelsen, Proofs Without Words II, MAA, 2000

Trigonometry

• What Is Trigonometry?
• Addition and Subtraction Formulas for Sine and Cosine
  • Sine of a Sum Formula
  • Addition and Subtraction Formulas for Sine and Cosine II
  • Addition and Subtraction Formulas for Sine and Cosine III
  • Addition and Subtraction Formulas
• The Law of Cosines (Cosine Rule)
• Cosine of 36 degrees
• Sine and Cosine of 15 Degrees Angle
• Sine, Cosine, and Ptolemy's Theorem
• arctan(1) + arctan(2) + arctan(3) = π
• arctan(1/2) + arctan(1/3) = arctan(1)
• Morley's Miracle
• Napoleon's Theorem
• A Trigonometric Solution to a Difficult Sangaku Problem
• Trigonometric Form of Complex Numbers
• Derivatives of Sine and Cosine
• ΔABC is right iff sin²A + sin²B + sin²C = 2
• Hunting Right Angles
• Point on Bisector in Right Angle
• Trigonometric Identities with Arctangents
• The Concurrency of the Altitudes in a Triangle - Trigonometric Proof

Proofs Without Words

• Proofs Without Words
• Sums of Geometric Series - Proofs Without Words
• Sine of the Sum Formula
• Parallelogram Law: A PWW
• Parallelogram Law
• Ceva's Theorem: Proof Without Words
• Viviani's Theorem
• A Property of Rhombi
• Triangular Numbers in a Square
• PWW: How Geometry Helps Algebra

|Activities| |Contact| |Front page| |Contents| |Algebra| |Store|