Lamé's Theorem - the Very First Application of Fibonacci Numbers
Among the unique properties of number five, Joe Roberts counts the appearance of five in one of the formulations of Lamé's theorem:
In carrying out the Euclidean algorithm to find the greatest common divisor of two positive integers \(a\) and \(b\), the number of steps needed will never exceed 5 times the number of base 10 digits in the smaller of the two integers \(a\) and \(b\).
Various aspects of this theorem, first proved by (Gabriel) Lamé in 1844, are quite regularly rediscovered. No doubt a "natural high" occurs each time this happens. (At least that was so in my case.)
In a 1992 publication, Roberts refers to a 1939 text on Number Theory, which tells me that Lamé's remarkable theorem is not very well known, at least among non-specialists. In his Mathematical Gems II, Ross Honsberger refers to the 1924 edition of W. Sierpinski book Elementary Theory of Numbers; the book has been republished twice since, but by now became a bibliographic rarity. It is available online for download as djvu file.
Lamé's theorem and the Euclidean algorithm have been discussed at length in the 1969 D. Knuth's Seminumerical Algorithms, now available in the third edition (1997) and lately in a most unusual book by V. H. Moll. So, we have three somewhat different formulations, each emphasizing a little different aspects of the theorem.
Lamé's Theorem (Honsberger)
The number of steps (i.e., divisions) in an application of the Euclidean algorithm never exceeds 5 times the number of digits in the lesser.
Lamé's Theorem (Knuth)
For \(n\ge 1\), let integers \(u\) and \(v\), \(u\gt v\gt 0\), be such that processing \(u\) and \(v\) by the Euclidean algorithm takes exactly \(n\) division steps. Moreover, assume that \(u\) is the least possible number satisfying that requirement. Then \(u=F_{n+2}\) and \(v=F_{n+1}\), where \(\{F_k\}\) is the Fibonacci sequence.
Knuth also proves
Corollary
For \(0\lt u,v\lt N\), the number of the division steps needed by the Euclidean algorithm to process \(u\) and \(v\) does not exceed \(\big\lceil log_{\phi}(\sqrt{5}N)\big\rceil -2\).
Lamé's Theorem (Moll)
Let \(a,b\in\mathbb{N}\) with \(a\gt b\). The number of steps in the Euclidean algorithm is about \(\mbox{log}_{10}b/\mbox{log}_{10}\phi\). This is at most five times the number of decimal digits of \(b\).
\(\phi\) here is of course the Golden Ratio (\(\displaystyle\phi = \frac{1+\sqrt{5}}{2}\)) whose appearance may not be surprising after the Fibonacci sequence made its debut in Knuth's formulation. In all the proofs the Fibonacci numbers play a most fundamental role and, as Knuth observes, this was their first ever practical application; many more followed.
On this page it is convenient to define the Fibonacci numbers recursively
\(F_n= \begin{cases} 1 & \mbox{if } n = 0; \\ 1 & \mbox{if } n = 1; \\ F_{n-1}+F_{n-2} & \mbox{if } n > 1. \\ \end{cases} \)
Let \(p_n\) denote the number of digits in \(F_n\). As R. L. Duncan showed in 1966, the number of the division steps in the Euclidean algorithm required to compute \(\mbox{gcd}(F_{n+1}, F_{n})\) always satisfies the inequality
\(\displaystyle n\gt\frac{p_n}{\mbox{log}_{10}\phi} - 5\)
while Lamé's result could be reformulated as \(\displaystyle n\lt\frac{p_n}{\mbox{log}_{10}\phi} + 1\). In 1967, J. L. Brown has proved a stronger result:
There exist an infinite number of distinct positive integers \(n\) such that the determination of \(\mbox{gcd}(F_{n+1},F_{n})\) by the Euclidean algorithm requires exactly \(n\) divisions with \(n\) satisfying
\(\displaystyle n\gt\frac{p_n}{\mbox{log}_{10}\phi} - \frac{1}{2}\),
making the estimate in Lamé's theorem the best possible.
All proofs of the above-mentioned results use but basic properties of the Fibonacci numbers. The Honsberger/Sierpinski one is based on the following
Lemma
For all \(n\ge 1\), \(F_{n+5}\gt 10\cdot F_{n}\).
Proof
From the basic recurrence, \(F_{k+2}=F_{k+1}+F_{k}\), \(F_{k+2}=2\cdot F_{k}+F_{k-1}\), so we obtain successively
\( \begin{align} F_{n+5} &= F_{n+4} + F_{n+3} \\ &= 2\cdot F_{n+3} + F_{n+2} \\ &= 3\cdot F_{n+2} + 2\cdot F_{n+1} \\ &= 5\cdot F_{n+1} + 3\cdot F_{n} \\ &= 8\cdot F_{n} + 5\cdot F_{n-1} \\ &= 13\cdot F_{n-1} + 8\cdot F_{n-2} \\ &= 21\cdot F_{n-2} + 13\cdot F_{n-3} \\ &> 10\cdot (2F_{n-2} + F_{n-3}) \\ &= 10\cdot F_{n}. \end{align} \)
From this it is immediate that \(F_{n+5}\) has at least one more decimal digit than \(F_n\). It follows by induction that \(p_{n+5t}\gt 10^{t}p_{n}\). By direct inspection, numbers \(F_n\), for \(1\le n\le 5\) are single-digit. They
have at least \(2\) digits for \(5\lt n\le 10\),
have at least \(3\) digits for \(10\lt n\le 15\),
have at least \(4\) digits for \(15\lt n\le 20\),
and, in general, have at least \(k\) digits for \(5(k-1)\lt n\le 5k\). In other words, for \(5(k-1)\lt n\le 5k\), \(p_{n}\ge k\ge n/5\). Thus it is always the case that \(p_{n}\ge n/5\).
Let's remember that; this in an important step in proving Lamé's theorem. But in order to complete the proof, we need to bring in the Euclidean algorithm.
Given to integers, \(a\) and \(b\), \(a\gt b\gt 0\), we set \(a = r_0\), \(b=r_1\) and divide with remainder. Assuming Euclid's algorithm takes \(n\) steps,
\( \begin{align} r_{0} &= r_{1}q_{1} + r_{2}, 0\le r_{2}\lt r_{1} \\ r_{1} &= r_{2}q_{2} + r_{3}, 0\le r_{3}\lt r_{2} \\ r_{2} &= r_{3}q_{3} + r_{4}, 0\le r_{4}\lt r_{3} \\ &= \cdots \\ r_{n-2} &= r_{n-1}q_{n-1} + r_{n}, 0\le r_{n}\lt r_{n-1} \\ r_{n-1} &= r_{n}q_{n}. \\ \end{align} \)
Note that \(q_{n}\ge 2\), for, otherwise, we would have \(r_{n-1} = r_{n}\), in contradiction with the previous step of the algorithm (\(0\le r_{n}\lt r_{n-1}\).) We now proceed backwards, starting with \(r_{n}\ge 1\), which implies \(r_{n}\ge F_{1}.\) Next, \(r_{n-1}\ge 2r_{n} = F_{2}.\) And further,
\(r_{n-2} = r_{n-1}q_{n-1} + r_{n} \gt r_{n-1} + r_{n} \gt F_{2} + F_{1} = F_{3}.\)
In general, for \(1\le k\le n\),
\( \begin{align} r_{n-k} &= r_{n-k+1}q_{n-k+1} + r_{n-k+2} \\ & \gt r_{n-k+1} + r_{n-k+2} \\ & \gt F_{k} + F_{k-1} = F_{k+1}, \end{align} \)
such that at the end of the process(i.e., at the beginning of the algorithm) when \(k=n-1\) and \(k=n\), \(b=r_{1}\gt F_{n}\) and \(a=r_{0}\gt F_{n+1}\). Therefore, if integers \(a\) and \(b\), \(a\gt b\gt 0\), are such that the Euclidean algorithm takes exactly \(n\) steps, then necessarily \(b\gt F_{n}\) and has at least as many digits, which, as we found previously, is at least \(n/5\). And this proves the Sierpinski/Honsberger formulation.
Now, for Moll's formulation. Recollect that \(\phi ^{2}=\phi + 1\). We use that to prove by induction another
Lemma
For \(n\gt 1\), \(F_{n}\gt \phi ^{n-1}.\)
Proof
Although, the statement is to be proved for \(n\gt 1\), it saves time to observe that \(F_{1}=1\ge \phi ^ {0}\). Also \(F_{2}=2\gt \phi ^1\). Then
\(F_{3} = F_{2} + F_{1} \gt 1 + \phi = \phi ^{2}.\)
And, in general,
\(F_{k+2} = F_{k+1} + F_{k} \gt \phi ^{k} + \phi ^{k-1} = \phi ^{k-1} (1 + \phi) = \phi ^{k-1} \phi ^{2} = \phi ^{k+1}.\)
Now, as we already found, if, for \(a\) and \(b\), \(a\gt b\gt 0\), the Euclidean algorithm takes \(n\) steps, then \(b\gt F_{n}\) so that \(b\gt \phi ^{n-1}\), and \(n-1 \lt \frac{\mbox{log}_{10}b}{\mbox{log}_{10}\phi}\). If \(b\) is a \(k\)-digit integer, then \(10^{k-1}\le b\lt 10^k\), and since \(1/\mbox{log}_{10}(\phi)=4.78497...\), \(n-1\lt 5k\), or \(n\le 5k\). This exactly means that the number of the division steps in an application of Euclidean algorithm is at most five times the number of decimal digits of the smaller of the two numbers the algorithm has been applied to.
Almost obviously a pair of consecutive Fibonacci numbers provide a "worse case scenario" - the longest possible application of the Euclidean algorithm relative to the length of the numbers. This is because the quotients \(q_k\) in the application of the algorithm in this case are all 1 (meaning the least reduction in length), except of course the last one.
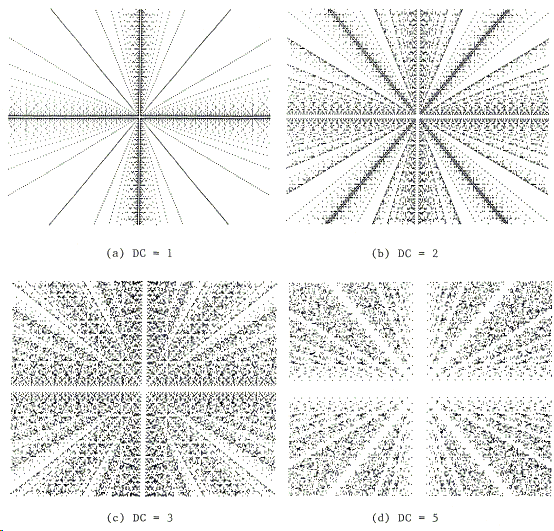
Finally, T. E. Moore has investigated the distribution of pairs \((a ,b)\) for a given number of steps (DC = "division count") in the Euclidean algorithm. The article includes a Basic programs that has been run on an Apple computer! Adding a 4-fold symmetry, Moore produced a sequence of mysterious diagrams:
References
- J. L. Brown, Jr., On Lamé's Theorem, Fibonacci Quarterly, v 5, n 2 (April 1967), 153-160
- R. L. Duncan, Note on the Euclidean Algorithm, The Fibonacci Quarterly, v 4, n 4, (August 1966) 367-68.
- R. Honsberger, Mathematical Gems II, MAA, 1976
- D. Knuth, The Art of Computer Programming, v2, Seminumerical Algorithms, Addison-Wesley, 1997 (3rd edition)
- V. H. Moll, Numbers and Functions: From a Classical-Experimental Mathematician's Point of View, AMS, 2012
- T. E. Moore, Euclid's Algorithm and Lamé's Theorem on a Microcomputer, Fibonacci Quarterly, v 27, n 4 (August 1989), 290-295
- J. Roberts, Lure of the Integers, MAA, 1992
- W. Sierpinski, Elementary Theory of Numbers: Second English Edition, North Holland, 1988
- J. V. Uspensky & M. A. Heaslet. Elementary Number Theory, McGraw-Hill, 1939.
- Modular Arithmetic
- Chinese Remainder Theorem
- Euclid's Algorithm
- Euclid's Algorithm (An Interactive Illustration)
- Euclid's Game
- Extension of Euclid's Game
- Binary Euclid's Algorithm
- gcd and the Fundamental Theorem of Arithmetic
- Extension of Euclid's Algorithm
- Lame's Theorem - First Application of Fibonacci Numbers
- Stern-Brocot Tree
- Farey series
- Pick's Theorem
- Fermat's Little Theorem
- Wilson's Theorem
- Euler's Function
- Divisibility Criteria
- Examples
- Equivalence relations
- A real life story
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny
73798523
