Horner's Method

Horner's method (also Horner Algorithm and Horner Scheme) is an efficient way of evaluating polynomials and their derivatives at a given point. It is also used for a compact presentation of the long division of a polynomial by a linear polynomial. The method is named after the British mathematician William George Horner (1786 - 1837).

A polynomial P(x) can be written in the descending order of the powers of x:

P(x) = a_nxⁿ + a_n-1x^n-1 + ... + a₁x + a₀

or in the ascending order of the exponents:

P(x) = a₀ + a₁x + ... + a_n-1x^n-1 + a_nxⁿ.

The Horner scheme computes the value P(t) of the polynomial P at x = t as the sequence of steps starting with the leading coefficient a_n:

(1)	bk = t·bk+1 + ak,

k = n - 1, n - 2, ..., 1, 0 and b_n = a_n, with b₀ = P(t). This follows from a special form of the polynomial

P(x) = ( ... (a_nx + a_n-1) x + ... + a₁) x + a₀

in the descending order of the exponents or in the ascending order as in

P(x) = a₀ + x (a₁ + x (a₂ + x (... + x (a_n-1 + x a_n) ... ).

For example, the polynomial P(x) = 2x⁴ - 3x³ + x + 7 can be written as

P(x) = (((2x - 3) x + 0) x + 1) x + 7,

or else as

P(x) = 7 + x (1 + x (0 + x (-3 + x·2))).

According to (1), say P(2) comes out as the last term in the sequence

b4	= a4	= 2
b3	= 2·b4 + a3	= 1
b2	= 2·b3 + a2	= 2
b1	= 2·b2 + a1	= 5
b0	= 2·b1 + a0	= 17

These calculations are conveniently arranged into a table

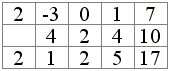
or, in the ascending order, with calculations carried right to left,

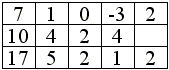
where the first row lists the coefficients of the polynomial, the third row the sequence of computed b_i's. The auxiliary quantities 2·b_i's are placed diagonally from b_i's and under the a_i-1 they are summed with according to (1). Thus we see that P(2) = 17, the last of the b's.

The other terms in the last row also come in handy. By direct verification one can check that

P(x) = 2x⁴ - 3x³ + x + 7 = (x - 2)(2x³ + x² + 2x + 5) + 17.

So the coefficients b in the last row comprise both the quotient of the division of P(x) by (x - 2), viz. Q(x) = 2x³ + x² + 2x + 5, and the remainder 17. In fact if you carry out the multiplication (x - 2)Q(x) and observe the manner in which the like powers of x combine, you could not help but notice an additional justification for the algorithm (1).

Note also that P(x) = (x - 2)Q(x) + 17 implies P(2) = 17. This follows by substitution P(2) = (2 - 2)Q(2) + 17 and holds true regardless of the value Q(2). However the latter is also a meaningful quantity as we shall see shortly.

The applet below helps finding more examples of the workings of the Horner scheme. All blue numbers (the coefficients of P, the highest power of x and the specific value of x in the third line are clickable. Click on both sides of their vertical midline to see how they change.)

---

This applet requires Sun's Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun's website at https://www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet.

---

What if applet does not run?

Let's now see what additional use can be made of the quantity Q(t) in

(2)	P(x) = (x - t)Q(x) + r,

where Q(x) is the quotient of P(x) / ( x - t) and r is the remainder. Both appear in the third row of the Horner scheme. This material is intended for the beginning Calculus students. Let's differentiate (2). By the product rule,

P'(x)	= [(x - t)Q(x) + r]'
	= (x - t)'Q(x) + (x - t)Q'(x)
	= Q(x) + (x - t)Q'(x).

It follows that

P'(t)	= Q(t) + (t - t)Q'(t)
	= Q(t).

Using the example of P(x) = 2x⁴ - 3x³ + x + 7, we see that, in addition to P(2) = 17, we can obtain P'(2) by computing the quotient Q(x) = 2x³ + x² + 2x + 5 for x = 2, for P'(2) = Q(2). This calls for appending additional two rows two the Horner table to allow computing of Q(2) with the help of the Horner scheme.

References

1. K. Atkinson, Elementary Numerical Analysis, John Wiley & Sons, 1985

|Contact| |Front page| |Contents| |Algebra|

Copyright © 1996-2018 Alexander Bogomolny