Hiroshi Haruki's Lemma
What is this about?
A Mathematical Droodle

The applet may suggest the following assertion:

Assume $AB\,$ and $CD\,$ are two chords and $P\,$ a point on a circle. Let $Q\,$ and $R\,$ be the intersections of $PC\,$ and $PD\,$ with $AB.\,$ Draw circumcircles of triangles $PRC\,$ and $PQD\,$ and let $AB\,$ intersect the two circles in $F\,$ and $E,\,$ respectively.

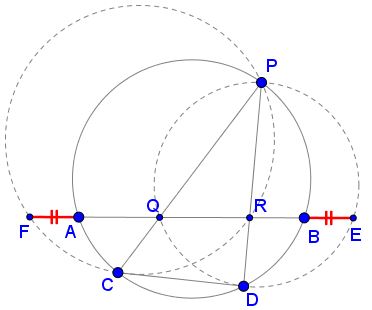
Haruki's lemma, illustration

Then

(1)

$BE = AF,\,$ and their length does not depend on the position of $P\,$ on the given circle.

The latter is an unintended consequence of the proof of Hiroshi Haruki's Lemma [Honsberger]:

(2)

For $AB, CD, P, Q, R\,$ as above, $\displaystyle \frac{AQ\cdot RB}{QR}\,$ does not depend on the position of $P\,$ on the given circle.

Proof

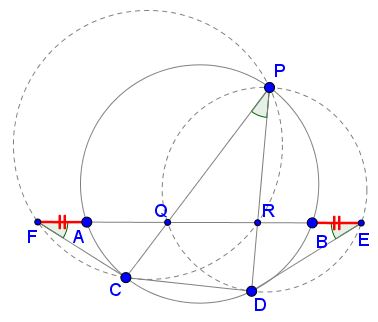
Haruki's lemma

In the circumcircle $PQD,\,$ if $P\,$ lies in the major arc $CD,\,$ the angles $QPD\,$ and $QED\,$ are equal as subtending the same chord $QD.\,$ As $P\,$ traverses the major arc $CD,\,$ the angle at $E\,(AED)\,$ remains the same, which means that the point $E\,$ remains fixed. (This is in fact true even if $P\,$ lies on the minor arc $CD.)\,$ So that $BE = const,\,$ independent of the position of $P\,$ on the circle.

We apply the intersecting Chords Theorem to $PD\,$ crossed by $AE\,$ in two circles:

$PR\cdot RD = QR\cdot RE\,$ and $PR\cdot RD = AR\cdot RB,\,$

from which

$\displaystyle QR\cdot (RB + BE) = (AQ + QR)\cdot RB,$

or $QR\cdot BE = AQ\cdot RB,\,$ and finally

(3)

$\displaystyle \frac{AQ\cdot RB}{QR} = BE.$

This proves (2) and also (1), since a similar argument in the circle $PRC\,$ shows that $F\,$ is independent of $P\,$ and, in addition, $\displaystyle AF = \frac{AQ\cdot RB}{QR},\,$ the same expression as in (3).

The lemma leads to elegant proofs of the Butterfly and Two Butterflies theorems.

References

Y. Bezverkhnyev, Haruki’s Lemma and a Related Locus Problem, Forum Geometricorum, Volume 8 (2008) 63–72.
R. Honsberger, The Butterfly Problem and Other Delicacies from the Noble Art of Euclidean Geometry I, TYCMJ, 14 (1983), pp. 2-7.
R. Honsberger, Mathematical Diamonds, MAA, 2003, pp. 136-140

71529972

Hiroshi Haruki's LemmaWhat is this about? A Mathematical Droodle

Proof

References

Hiroshi Haruki's Lemma
What is this about?
A Mathematical Droodle