Sums of Squares in Circle
Source
Leo Giugiuc has kindly posted at the CutTheKnotMath facebook page a problem due to Miguel Ochoa Sanchez:
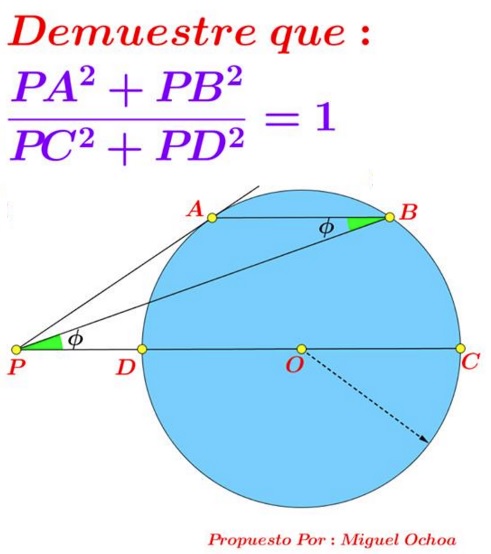
Problem
Chord $AB\;$ in a circle is parallel to the diameter $CD.\;$ The tangent at $A\;$ meets $CD\;$ extended at $P.$
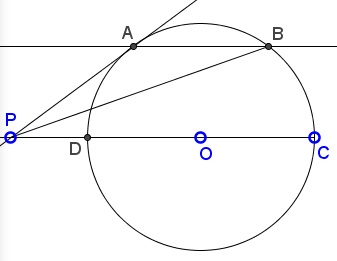
Prove that $\displaystyle AP^2+BP^2 = CP^2+DP^2.$
Solution 1
Let $D=(-1,0),\;$ $C=(1,0),\;$ $A=(-cos t,\sin t),\;$ and $B=(\cos t,\sin t),\;$ $\displaystyle 0\lt t\lt\frac{\pi}{2}.\;$ The tangent at $A\;$ is described by the equation $-x\cos t+y\sin t=1,\;$ from which $\displaystyle P=\left(-\frac{1}{\cos t},0\right).\;$ Furthermore, $\displaystyle CP^2+DP^2 = 2+\frac{2}{\cos^2 t}\;$ and $\displaystyle AP^2+BP^2=\left(\cos t-\frac{1}{\cos t}\right)^2+\sin^2t+\left(\cos t+\frac{1}{\cos t}\right)^2+\sin^2t=2+\frac{2}{\cos^2t}.$
Solution 2
I'd do this one with vectors. First observe that $a^2 = b^2 = c^2 = d^2 = r^2,\;$ where $r\;$ is the radius of the circle. Also note that $(a + b)\cdot p = 0\;$ because $a+b\;$ is perpendicular to $p,\;$ and that $(c + d)\cdot p = 0\;$ because $c+d\;$ is zero. Now
$\displaystyle\begin{align} PA^2 + PB^2 &= (a - p)^2 + (b - p)^2\\ &= a^2 - 2 a\cdot p + p^2 + b^2 - 2 b\cdot p + p^2\\ &= a^2 + b^2 - 2(a + b)\cdot p + 2 p^2\\ &= 2 r^2 - 0 + 2 p^2 = c^2 + d^2 - 2(c + d)\cdot p + 2 p^2\\ &= c^2 - 2 c\cdot p + p^2 + d^2 - 2 d\cdot p + p^2\\ &= (c - p)^2 + (d - p)^2 = PC^2 + PD^2. \end{align}$
Solution 3


Acknowledgment
Solution 1 is by Leo Giugiuc and Dan Sitaru; Solution 2 is by Tim Robinson; Solution 3 is by Miguel Ochoa Sanchez.
Butterfly Theorem and Variants
- Butterfly theorem
- 2N-Wing Butterfly Theorem
- Better Butterfly Theorem
- Butterflies in Ellipse
- Butterflies in Hyperbola
- Butterflies in Quadrilaterals and Elsewhere
- Pinning Butterfly on Radical Axes
- Shearing Butterflies in Quadrilaterals
- The Plain Butterfly Theorem
- Two Butterflies Theorem
- Two Butterflies Theorem II
- Two Butterflies Theorem III
- Algebraic proof of the theorem of butterflies in quadrilaterals
- William Wallace's Proof of the Butterfly Theorem
- Butterfly theorem, a Projective Proof
- Areal Butterflies
- Butterflies in Similar Co-axial Conics
- Butterfly Trigonometry
- Butterfly in Kite
- Butterfly with Menelaus
- William Wallace's 1803 Statement of the Butterfly Theorem
- Butterfly in Inscriptible Quadrilateral
- Camouflaged Butterfly
- General Butterfly in Pictures
- Butterfly via Ceva
- Butterfly via the Scale Factor of the Wings
- Butterfly by Midline
- Stathis Koutras' Butterfly
- The Lepidoptera of the Circles
- The Lepidoptera of the Quadrilateral
- The Lepidoptera of the Quadrilateral II
- The Lepidoptera of the Triangle
- Two Butterflies Theorem as a Porism of Cyclic Quadrilaterals
- Two Butterfly Theorems by Sidney Kung
- Butterfly in Complex Numbers
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73575060
