The Laws of Sines and Cosines
The Law of Sines establishes a relationship between the angles and the side lengths of ΔABC:
a/sin(A) = b/sin(B) = c/sin(C).
The relationship explains the plural "s" in Law of Sines: there are 3 sines after all. Another important relationship between the side lengths and the angles of a triangle is expressed by the Law of Cosines.
c² = a² + b² - 2ab·cos(C)
Why do we use the plural "s" in the Law of Cosines? The expression itself involves a single cosine, but by rotation (or, as A. Einstein might have said, by symmetry) similar formulas are valid for other angles:
a² = b² + c² - 2bc·cos(A) and b² = c² + a² - 2ca·cos(B)
In fact, I do not know the exact sources of the existing nomenclature. But there is another plurality involved with the Law of Cosines. Most of the proofs of the Law consider separately the cases of acute, right, and obtuse triangles. This is a manifestation of the fact that cosine, unlike sine, changes its sign in the range
The essence of the Law of Cosines has been known to Euclid, who proved the obtuse case as II.12 and the acute case as II.13. Here's how the former could be translated into plain English [Euclid, p. 403-404]:
In obtuse-angled triangles the square on the side subtending the obtuse angle is greater than the squares on the sides containing the obtuse angle by twice the rectangle contained by one of the sides about the obtuse angle, namely that on which the perpendicular falls, and the straight line cut off outside by the perpendicular towards the obtuse angle.
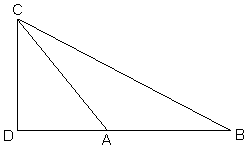
With the reference to the diagram on the right, Euclid's proof amounts to the following derivation.
By the Pythagorean theorem,
BC² = BD² + CD²,
AC² = AD² + CD².
Taking the difference we obtain,
| BC² - AC² | = BD² - AD² |
| = (BD - AD)·(BD + AD) | |
| = AB·(AB + 2AD) | |
| = AB² + 2AB·AD, |
which is II.12 in modern notations: BC² = AC² + AB² + 2AB·AD. (This is in fact the same proof as we used to show that the law of cosines is a direct consequence of a less general Pythagorean theorem. I am grateful to Douglas Rogers who suggested the reference to the Elements. Also, the latest formula has a slightly different form discovered by Larry Hoehn that generalizes the Pythagorean theorem in a little different way.)
Here's a couple of proofs from Proofs Without Words by Roger Nelsen [p. 32-33]. The first one uses the power of a point with respect to a circle theorem, the other the theorem of Ptolemy.

The first proof assumes that ![]() C is acute, the second that it's obtuse. (See if you can modify the diagrams to account for the remaining cases.)
C is acute, the second that it's obtuse. (See if you can modify the diagrams to account for the remaining cases.)
In Trigonometric Delights [p. 216-217] Eli Maor employs the notion of projection to prove both Laws.
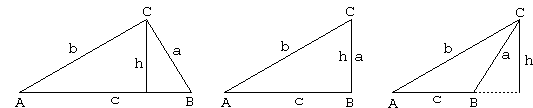
Taking projections of both AC and BC on the height h gives in all three cases
| (1) | a·sin(B) = b·sin(A) (= h) |
which proves the Law of Sines with additional identities obtained in a similar manner. (Einstein would probably rather avoid additional constructs by using a formula for the area S of a triangle: 2S = ab·sin(C) = bc·sin(A) = ca·sin(B).) If we take projections of AC and BC on AB the result will be
| (2) | c = a·cos(B) + b·cos(A) |
which is again the same in all three cases, although the sum here is algebraic: one of the terms may be negative or zero. Maor remarks that it would be entirely appropriate to call the latter identity the Law of Cosines because it does contain 2 cosines with an immediate justification for the plural "s".
The proof of the real Law now proceeds by squaring (2):
| c² | = a²(cos B)² + b²(cos A)² + 2ab·cos(A)·cos(B) |
| = a²(1 - (sin B)²) + b²(1 - (sin A)²) + 2ab·cos(A)·cos(B) | |
| = a² + b² - (a·sin(B))(a·sin(B)) - (b·sin(A))(b·sin(A)) + 2ab·cos(A)·cos(B) |
Plug in equation (1):
| c² | = a² + b² - a·sin(B)·b·sin(A) - a·sin(B)·b·sin(A) + 2ab·cos(A)·cos(B) |
| = a² + b² + 2ab(cos(A)cos(B) - sin(A)sin(B)) | |
| = a² + b² + 2ab(cos(A + B)) | |
| = a² + b² + 2ab(cos(180° - C)) | |
| = a² + b² - 2ab(cos(C)) |
A continuum of proofs for the Law of Cosines can be discovered by dissection [Plane & Fancy, p. 38]. (However, these do not seem to work for acute angles C.) The proofs generalize that of the Pythagorean theorem by K.O. Friedrichs. The plane is now tessellated into two families of parallelograms with sides a and b and smaller angles of (C - 90°) and squares of sides a and b.
| What if applet does not run? |
As mentioned by G. Frederickson [Plane & Fancy, p. 38-39], particular cases have been found by Rudolf Hunger (1921) and Erwin Dintzl (1931).
Of many other available proofs of the Law of Cosines, a proof without words is a direct generalization of Thâbit ibn Qurra's proof of the Pythagorean proposition. There is, as well, an "unfolded variant." Also, the Cosines Law admits a slightly different form discovered by Larry Hoehn that generalizes the Pythagorean theorem in a somewhat different way.
References
- G. N. Frederickson, Dissections: Plane & Fancy, Cambridge University Press, 1997
- T. L. Heath, Euclid: The Thirteen Books of the Elements, v. 1, Dover, 1956
- E. Maor, Trigonometric Delights, Princeton University Press, 1998
- R. B. Nelsen, Proofs Without Words, MAA, 1993
- The Law of Cosines (Cosine Rule)
- The Illustrated Law of Cosines
- The Law of Sines and Cosines
- The Law of Cosines: Plane Tessellation
- The Law of Cosines: after Thâbit ibn Qurra
- The Law of Cosines: Unfolded Version
- The Law of Cosines (Independent of the Pythagorean Theorem)
- The Cosine Law by Similarity
- The Law of Cosines by Larry Hoehn
- The Law of Cosines - Another PWW
- The Law of Cosines - Yet Another PWW
- Law of Cosines by Ancient Sliding
- The Cosine Law: PWW by S. Kung
![]()
|Contact| |Front page| |Contents| |Geometry| |Up|
Copyright © 1996-2018 Alexander Bogomolny73596223
