Two Butterflies Theorem
What is it about?
A Mathematical Droodle
Explanation
|Activities|
|Contact|
|Front page|
|Contents|
|Geometry|
|Eye opener|
|Store|
Copyright © 1996-2012 Alexander Bogomolny
Two Butterflies Theorem
The theorem below that might be called Two Butterflies Theorem is a generalization of a better known Butterfly Theorem.
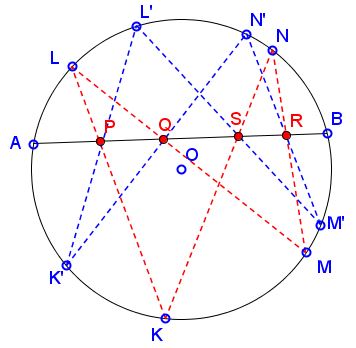
Let two self-intersecting quadrilaterals KLMN and K'L'M'N' be inscribed into the same circle. Assume the two intersect chord AB at points P, Q, R, S and P', Q', R', S', respectively. (P lies on KL, Q on LM, etc.) Assume also that none of the vertices of the quadrilaterals coincides with either A or B. If some three of the points P, Q, R, S coincide with three corresponding points out of P', Q', R', S' (e.g., P = P', Q = Q', R = R'), then the remaining two points also coincide.
Proof
As the main instrument in the proof, we' ll use a lemma that served as a basis for one of the proofs of the Butterfly theorem. According to that lemma, the circle at hand is defined by the equation f = 0, where
f = l lKLlMN + m lKNlML, and also
f = l' lK'L'lM'N' + m' lK'N'lM'L'.
Consider the line AB as a number line with a coordinate x. Assume for definiteness sake that P = P', Q = Q', and R = R'. Assume also that the points P, Q, R, S, and S' have coordinates p, q, r, s, and s', respectively. Then, restricted to the line AB, the above equations imply
a(x - p)(x - r) + b(x - q)(x - s) = a'(x - p)(x - r) + b'(x - q)(x - s').
We want to show that s = s'.
If a = a', then also b = b' and s = s' right away. But, by our convention (P lies on KL, Q on LM, etc.), Q may not equal either P or R, therefore, (x - p)(x - r) is not divisible by (x - q). Therefore, necessarily a = a', and we are finished.
There is an additional proof due to Nathan Bowler.
Let P be a point not on a circle C. Let fP be the transformation taking each point A on C to the other intersection of AP with C. Then there is a mobius transform gP such that fP is the restriction of gP to C.
Proof
If P lies outside C, then by the intersecting chords theorem we may take gP to be inversion in a circle of suitable radius centred at P. If P lies inside C, it is merely necessary to add an extra half-twist centred at P.
Now let g be the mobius transformation obtained by composing gP, gQ, gR and gS. Then g has three fixed points on C: A, B and K. So g is the identity on C and so g(K') = K'. The result follows.
Note that the same argument will give the following interesting porism as a generalisation:
Let A and B lie on a circle S, and let P1, ... P2n be points on AB distinct from A and B. If there is any point K on S, other than A or B, with the property that there are points K1, ... K2n+1 on S with Pi lying on Ki Ki+1 for all i≤ 2n, and K1 = K2n+1 = K, then all points on S have this property.
Remark
We may generalise still further. The key point to note is that in the lemma we may in fact construct gP knowing only P, A and B where P, A and B are collinear and A and B lie on the circle C. Then, clarifying the proof by noting that g preserves the orientation of the plane and so is not the identity merely on C but everywhere, we may observe that it is not necessary for the circles KLMN and K'L'M'N' to be the same; we need only require that both pass through both A and B.
To be less formal, in the two butterflies theorem the two butterflies may live on different circles, provided that those circles meet at A and B.
As a further generalization, it comes out that the two circles need not intersect: the theorem remains valid as long as A and B lie on the radical axis of the two circles.
Finally, like, say, Pascal's theorem, the theorem discussed here, deals only with incidence of points and lines and, therefore, is true for any non-degenerate conic. We have a demonstration of that statement for ellipses along with a demonstration of porism suggested by Nathan Bowler.
We have an additional proof of the main result. The proof is by L. Hoehn of a statement first proved by D. Jones.
With a reference to the above diagram, Jones' result appears as
| |
Let PQ be a fixed chord of a circle and let "butterfly R" and "butterfly S" be inscribed in the circle and oriented such that their wings cut PQ (in order from left to right) at R4, R3, R2, R1 and S1, S2, S3, S4, respectively. If PR1 = QS1, PR2 = QS2 and PR3 = QS3, then PR4 = QS4.
|
(A reflection in the perpendicular bisector of PQ immediately shows that the "Double Butterfly Theorem" is equivalent to the "Two Butterflies Theorem".)
We apply Hiroshi Haruki's Lemma twice. For the proof of the theorem we let m = PR4, n = QS4, a = PR3 = QS3, b = R3R2 = S3S2, c = R2R1 = S2S1, d = R1S1, and e = a + b + c + d.
By applying Haruki's lemma twice to points A and B and fixed chords PQ and CD of butterfly R, we have
m·(b + c + e) / (a - m) = (a + b)·e / c,
sine both are equal to the same constant. Similarly,
| |
m·(b + c + e) / (a - n) = (a + b)·e / c,
|
for butterfly S. By transitivity of equality, we easily get m = n, which completes the proof.
References
- D. Jones, A Double Butterfly Theorem, Math Magazine 49 (1976), pp. 86-87
- L. Hoehn, A New Proof of the Double Butterfly Theorem, Math Magazine 63 (1990), pp. 256-257
- V. V. Prasolov, Essays On Numbers And Figures, AMS, 2000
Butterfly Theorem and Variants
- Butterfly theorem
- 2N-Wing Butterfly Theorem
- Better Butterfly Theorem
- The Lepidoptera of the Circles
- The Lepidoptera of the Quadrilateral
- The Lepidoptera of the Quadrilateral II
- Butterflies in Ellipse
- Butterflies in Hyperbola
- Butterflies in Quadrilaterals and Elsewhere
- Pinning Butterfly on Radical Axes
- Shearing Butterflies in Quadrilaterals
- The Plain Butterfly Theorem
- Two Butterflies Theorem
- Two Butterflies Theorem II
- Two Butterflies Theorem III
- Algebraic proof of the theorem of butterflies in quadrilaterals
- William Wallace's Proof of the Butterfly Theorem
- Butterfly theorem, a Projective Proof
|Activities|
|Contact|
|Front page|
|Contents|
|Geometry|
|Eye opener|
|Store|
Copyright © 1996-2012 Alexander Bogomolny
|
