cos 75 + cos 45 = cos 15
Problem
The purpose of this page is to establish the identity
$\cos 45^{\circ}+\cos 75^{\circ}=\cos 15^{\circ}$
which was posted by Imad Zak to the CutTheKnotMath facebook page along with a solution (Solution 1).
Solution 1
Using the well known formula $\displaystyle\cos\alpha -\cos\beta=-2\sin\frac{\alpha +\beta}{2}\sin\frac{\alpha-\beta}{2},\;$ we obtain
$\displaystyle\begin{align} \cos 15^{\circ}-\cos 75^{\circ} &= -2\sin\frac{15^{\circ}+75^{\circ}}{2}\sin\frac{15^{\circ}-75^{\circ}}{2}\\ &=2\sin 45^{\circ}\sin 30^{\circ}\\ &=2\cdot \frac{\sqrt{2}}{2}\cdot \frac{1}{2}\\ &=\frac{\sqrt{2}}{2}\\ &=\cos 45^{\circ}. \end{align}$
Solution 2
Elsewhere, based on Larry Hoehn's diagram,

we obtained
$\displaystyle \cos 75^{\circ}=\sin 15^\circ = \frac{\sqrt{6} - \sqrt{2}}{4}$
and
$\displaystyle \cos 15^\circ = \frac{\sqrt{6} + \sqrt{2}}{4}.$
Thus, $\displaystyle \left( \frac{\sqrt{6} + \sqrt{2}}{4}\right)-\left( \frac{\sqrt{6} - \sqrt{2}}{4}\right)=\frac{\sqrt{2}}{2}=\cos 45^{\circ}.$
Note that the Larry Hoehn's diagram presents a proof without words of this result: indeed, $AC=BC=2\cos 15^{\circ},\;$ $CD=2\cos 75^{\circ},\;$ and, finally, $AD=\sqrt{2}=2\cos 45^{\circ}.\;$ Thus the identity in the title follows from $AD+CD=AC.$
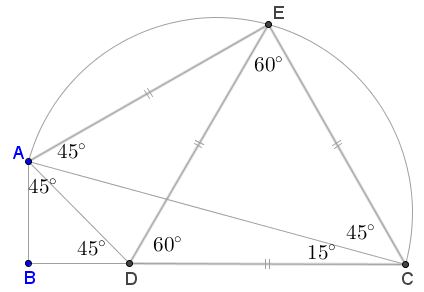
Solution 3
Here's another proof without words (that may still need a few words of explanation, assisted by angle chasing.) In the diagram, $AC=1,\;$ $BD=BC=\cos 75^{\circ},\;$ $AD=\cos 45^{\circ},\;$ and $AB=\cos 15^{\circ}.$
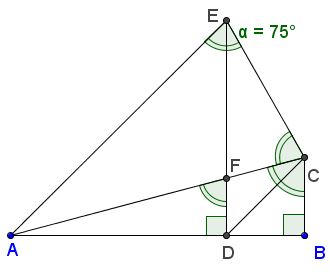
The construction proceeds in the following steps:
$\Delta ABC,\;$ with $\angle ABC=90^{\circ}\;$ and $\angle ACB=75^{\circ}.\;$ This makes $\angle BAC=15^{\circ}.$
$\Delta ACE,\;$ with $\angle ACE=\angle AEC=75^{\circ}.\;$ This makes $\angle CAE=30^{\circ}\;$ and $\angle DAE=45^{\circ}.$
$BD=BC.$
$FD\perp AB$ ($F\in AC)\;$ which makes $\angle AFD=75^{\circ}.$
$EF',$ $F'\in AC,\;$ with $\angle CEF'=30^{\circ},\;$ which makes $\angle CF'E=75^{\circ},\;$ implying $F=F'.$
The required identity follows from $AD+BD=AB,$
Solution 4
This PWW is by Dan Lawson:
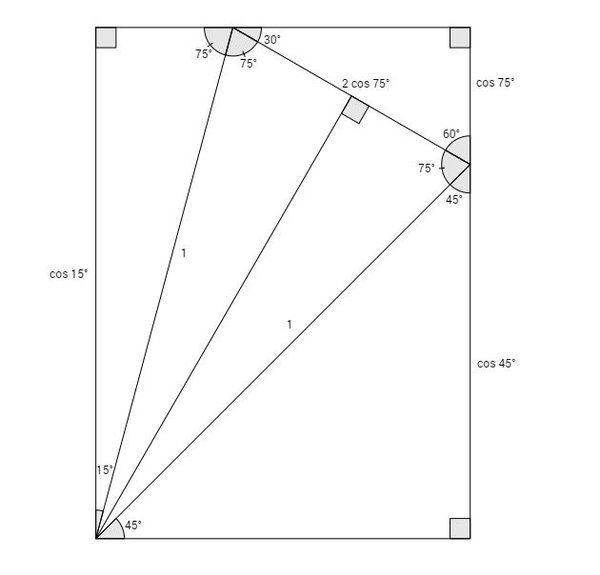
Generalization
Dan Lawson also supplied a PWW generalization: $\cos\alpha +\cos(120^{\circ}-\alpha )=\cos(\alpha-60^{\circ}):$
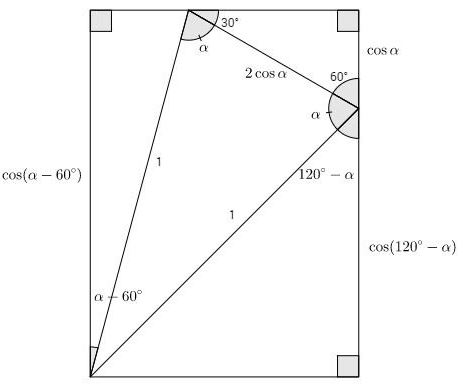
Solution 5
This solution was anonymously left in comments:
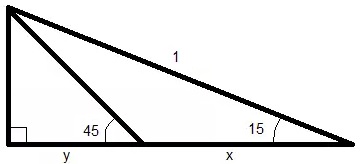
In the diagram, $y=\cos 75^{\circ},\;$ while $x\;$ could be found from the Law of Sines: $\displaystyle\frac{1}{\sin 135^{\circ}}=\frac{x}{\sin 30^{\circ}},\;$ such that $\displaystyle x=\frac{\sqrt{2}}{2}=\cos 45^{\circ}.$
Solution 6
This is an attempt to present the previous proof without trigonometry:
Trigonometry
- What Is Trigonometry?
- Addition and Subtraction Formulas for Sine and Cosine
- The Law of Cosines (Cosine Rule)
- Cosine of 36 degrees
- Tangent of 22.5o - Proof Wthout Words
- Sine and Cosine of 15 Degrees Angle
- Sine, Cosine, and Ptolemy's Theorem
- arctan(1) + arctan(2) + arctan(3) = π
- Trigonometry by Watching
- arctan(1/2) + arctan(1/3) = arctan(1)
- Morley's Miracle
- Napoleon's Theorem
- A Trigonometric Solution to a Difficult Sangaku Problem
- Trigonometric Form of Complex Numbers
- Derivatives of Sine and Cosine
- ΔABC is right iff sin²A + sin²B + sin²C = 2
- Advanced Identities
- Hunting Right Angles
- Point on Bisector in Right Angle
- Trigonometric Identities with Arctangents
- The Concurrency of the Altitudes in a Triangle - Trigonometric Proof
- Butterfly Trigonometry
- Binet's Formula with Cosines
- Another Face and Proof of a Trigonometric Identity
- cos/sin inequality
- On the Intersection of kx and |sin(x)|
- Cevians And Semicircles
- Double and Half Angle Formulas
- A Nice Trig Formula
- Another Golden Ratio in Semicircle
- Leo Giugiuc's Trigonometric Lemma
- Another Property of Points on Incircle
- Much from Little
- The Law of Cosines and the Law of Sines Are Equivalent
- Wonderful Trigonometry In Equilateral Triangle
- A Trigonometric Observation in Right Triangle
- A Quick Proof of cos(pi/7)cos(2.pi/7)cos(3.pi/7)=1/8
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73576834
