Two Butterflies Theorem

Sidney H. Kung
June 2015

Theorem 1

Let $I\,$ be the point of intersection of two chords $AB\,$and $CD\,$ in a circle $(O).\,$ Construct a diameter $JK\,$ through $I\,$ that does not intersect either $AD\,$ or $BC\,$ so that points $J\,$ and $I\,$ lie on the opposite sides of chord $AC.\,$ Let $BA\cap CJ=M,\,$ $DC\cap AJ=N,\,$ $AC\cap JK=H.\,$

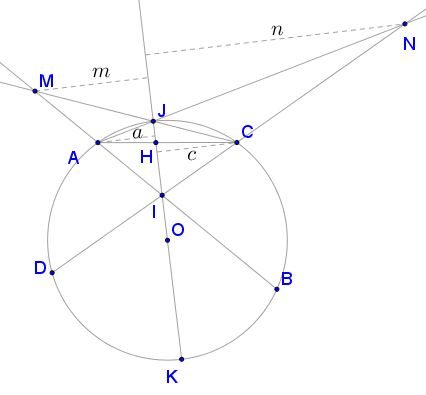
Two Butterfly Theorems by Sidney Kung

If the distances from points $A,\,$ $N\,$ $C,\,$ $M\,$ to the line $JK\,$ are $a,\,$ $n,\,$ $c,\,$ $m,\,$ respectively, then

$\displaystyle \frac{1}{a}+\frac{1}{n}=\frac{1}{c}+\frac{1}{m}.$

Proof of Theorem 1

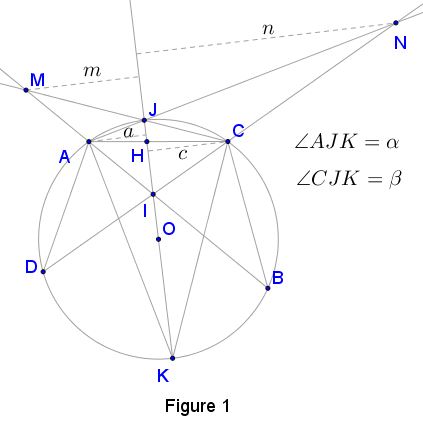
Two Butterfly Theorems by Sidney Kung, Figure 1

With a reference to Figure 1, $\angle JHC=\angle KHA\,$ and $\angle JCH=\angle AKH.\,$ So, triangles $JCH\,$ and $AKH\,$ are similar. In particular,

(1)

$\displaystyle \frac{JC}{AK}=\frac{JH}{AH}.$

Triangles $JAH\,$ and $CKH\,$ are also similar. In particular,

(2)

$\displaystyle \frac{JA}{CK}=\frac{JH}{CH}.$

Dividing (1) by (2), we have

(3)

$\displaystyle \frac{JC}{AK}\cdot\frac{CK}{JA}=\frac{CH}{AH}.$

Observe that point i does not lie on any of the three side lines of $\Delta JCA;\,$ and, since $IA\cap CJ=M,\,$ $IC\cap AJ=N\,$ and $IJ\cap AC=H,\,$ then by Menelaus' theorem $(\Delta ACM,\,$ transversal $HJ;\,$ $\Delta AMJ,\,$ transversal $NC),$

(3')

$\displaystyle \frac{JM}{MC}\cdot\frac{CH}{HA}\cdot\frac{AN}{NJ}=1$

or,

(4)

$\displaystyle \frac{CM}{AN}\cdot\frac{JN}{JM}=\cdot\frac{CH}{AH}.$

Equating (3) and (4) gives

(5)

$\displaystyle \frac{JC}{AK}\cdot\frac{CK}{JA}=\frac{CM}{AN}\cdot\frac{JN}{JM}.$

In Figure 1, let $\angle AJK=\alpha,\,$ $\angle CJK=\beta.\,$ Then $CK=JK\cdot\sin\beta,\,$ $AK=JK\cdot\sin\alpha.\,$ Substituting into (5) and rearranging terms we get

$\displaystyle \frac{AN}{JA\cdot JN\cdot\sin\alpha}=\frac{CM}{JC\cdot JM\cdot\sin\beta}$

i.e., $\displaystyle \frac{JN+AJ}{JA\cdot JN\cdot\sin\alpha}=\frac{JM+JM}{JC\cdot JM\cdot\sin\beta},\,$ or

$\displaystyle \frac{1}{JA\cdot\sin\alpha}+\frac{1}{JN\cdot\sin\alpha}=\frac{1}{JC\cdot\sin\beta}+\frac{1}{JM\cdot\sin\beta}.$

Hence $\displaystyle \frac{1}{a}+\frac{1}{n}=\frac{1}{c}+\frac{1}{m}$ as required.

Theorem 2

Let $I\,$ be the point of intersection of two chords $AB\,$and $CD\,$ in a circle $(O).\,$ Construct a diameter $JK\,$ through $I\,$ that does not intersect either $AD\,$ or $BC\,$ so that points $J\,$ and $I\,$ lie on the same sides of chord $AC.\,$ Let $AI\cap JC=G,\,$ $CI\cap AJ=F,\,$ $JI\cap CA=H.\,$

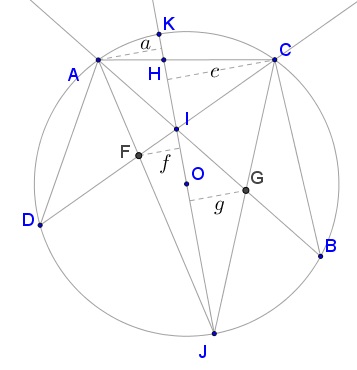
Two Butterfly Theorems by Sidney Kung, theorem 2

If the distances from points $G,\,$ $C\,$ $F,\,$ $A\,$ to the line $JK\,$ are $g,\,$ $c,\,$ $f,\,$ $a,\,$ respectively, then

$\displaystyle \frac{1}{g}-\frac{1}{c}=\frac{1}{f}-\frac{1}{a}.$

Proof of Theorem 2

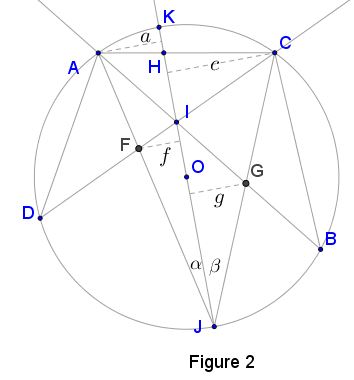
Two Butterfly Theorems by Sidney Kung, Figure 2

With a reference to Figure 2, $\Delta JAH\sim\Delta CKH,$ and $\Delta JCH\sim\Delta AKH.\,$ It follows that

(1)

$\displaystyle \frac{JA}{CK}=\frac{JH}{CH}.$

(2)

$\displaystyle \frac{JC}{AK}=\frac{JH}{AH}.$

Dividing (1) by (2), we have

(3)

$\displaystyle \frac{JC}{AK}\cdot\frac{CK}{JK}=\frac{CH}{AH}.$

In $\Delta JAC,\,$ the cevians $CF,\,$ $AG,\,$ and $JH\,$ are concurrent, thus, by Ceva's theorem,

(3')

$\displaystyle \frac{JF}{FA}\cdot\frac{AH}{HC}\cdot\frac{CG}{GJ}=1,$

or,

(4)

$\displaystyle \frac{CH}{AH}=\frac{JF}{FA}\cdot\frac{CG}{GJ}.$

Equating (3) and (4), we get

(5)

$\displaystyle \frac{JC}{AK}\cdot\frac{CK}{JA}=\frac{JF}{FA}\cdot\frac{CG}{GJ}.$

From Figure 2, $AK=JK\cdot\sin\alpha,\,$ $CK=JK\cdot\sin\beta.\,$ Substituting into (5) and rearranging terms, we have

$\displaystyle \frac{CG}{JC\cdot JG\cdot\sin\beta}=\frac{AF}{JA\cdot JF\cdot\sin\alpha},$

implying

$\displaystyle \frac{JC-JG}{JC\cdot JG\cdot\sin\beta}=\frac{JA-JF}{JA\cdot JF\cdot\sin\alpha},$

i.e.,

$\displaystyle \left(\frac{1}{JG}-\frac{1}{JC}\right)\cdot\frac{1}{\sin\beta}= \left(\frac{1}{JF}-\frac{1}{JA}\right)\cdot\frac{1}{\sin\alpha}.$

Hence, $\displaystyle \frac{1}{g}-\frac{1}{c}=\frac{1}{f}-\frac{1}{a},\,$ as required.

Butterfly Theorem and Variants

71548560