The Radical Axis of Circles Inscribed in a Circular Segment: What is this about?
A Mathematical Droodle
| What if applet does not run? |
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
The Radical Axis of Circles Inscribed in a Circular Segment
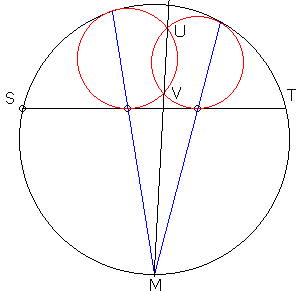
The applet suggests the following statement:
| (1) | A chord ST is drawn in a circle C with center O. Two circle C' and C'' are inscribed into the circular segment thus obtained. Assume C' and C'' intersect at the points U and V and let M denote the midpoint of the arc defined by ST opposite the segment. Then U, V, and M are collinear. |
In order to prove (1), let's establish the following identity
| (2) | MA·MB = MT2. |
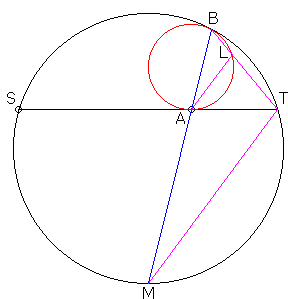
Circles C and C' are homothetic with center B, such that A, B, and M are collinear. Triangles BTM and MAT are similar. Indeed, the two triangles share an angle at M. Also, ∠BTM equals half the measure of the arc BSM. On the other hand, ∠MAT equals half the measure of the sum of arcs BS and MT, but the latter is equal to MS. Therefore,
From the similarity of triangles BTM and MAT we obtain
Now for the proof of (1). Observe that (2) holds for both C' and C'', as it does for any circle inscribed into the given circular segment. This means that M has the same power with respect to C' as it has with respect to C''. The points with that property lie on the radical axis of the two circles. The radical axis of two intersecting circles (that contains M) is the line that passes through the two points of intersection of C' and C''.
(The problem also has a simple interpretation in terms of the inversion transformation. See Problem 3 in the Inversion page.)
Radical Axis and Radical Center
- How to Construct a Radical Axis
- A Property of the Line IO: A Proof From The Book
- Cherchez le quadrilatere cyclique II
- Circles On Cevians
- Circles And Parallels
- Circles through the Orthocenter
- Coaxal Circles Theorem
- Isosceles on the Sides of a Triangle
- Properties of the Circle of Similitude
- Six Concyclic Points
- Radical Axis and Center, an Application
- Radical axis of two circles
- Radical Axis of Circles Inscribed in a Circular Segment
- Radical Center
- Radical center of three circles
- Steiner's porism
- Stereographic Projection and Inversion
- Stereographic Projection and Radical Axes
- Tangent as a Radical Axis
- Two Circles on a Side of a Triangle
- Pinning Butterfly on Radical Axes
- Two Lines - Two Circles
- Two Triples of Concurrent Circles
- Circle Centers on Radical Axes
- Collinearity with the Orthocenter
- Six Circles with Concurrent Pairwise Radical Axes
- Six Concyclic Points on Sides of a Triangle
- Line Through a Center of Similarity
Inversion - Introduction
- Angle Preservation Property
- Apollonian Circles Theorem
- Archimedes' Twin Circles and a Brother
- Bisectal Circle
- Chain of Inscribed Circles
- Circle Inscribed in a Circular Segment
- Circle Inversion: Reflection in a Circle
- Circle Inversion Tool
- Feuerbach's Theorem: a Proof
- Four Touching Circles
- Hart's Inversor
- Inversion in the Incircle
- Inversion with a Negative Power
- Miquel's Theorem for Circles
- Peaucellier Linkage
- Polar Circle
- Poles and Polars
- Ptolemy by Inversion
- Radical Axis of Circles Inscribed in a Circular Segment
- Steiner's porism
- Stereographic Projection and Inversion
- Tangent Circles and an Isosceles Triangle
- Tangent Circles and an Isosceles Triangle II
- Three Tangents, Three Secants
- Viviani by Inversion
- Simultaneous Diameters in Concurrent Circles
- An Euclidean Construction with Inversion
- Construction and Properties of Mixtilinear Incircles
- Two Quadruplets of Concyclic Points
- Seven and the Eighth Circle Theorem
- Invert Two Circles Into Equal Ones
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73506767
