CHASLES' THEOREM

By Hubert Shutrick

1. Pencils of Lines

Let f_s = a_sx + b_sy + c and f_t = a_tx + b_ty + c where f_s = 0 and f_t = 0 are two different straight lines in the plane. Each pair s, t such that (s, t) ≠ (0, 0) defines a line

sf_s + tf_t = 0,

and these lines form a pencil of lines with base f_s, f_t. For r ≠ 0, the parameters (rs, rt) give the same line as (s, t) and so the parameters are homogeneous. If the lines f_s = 0 and f_t = 0 have a common point, then any line in the pencil also goes through the point. Conversely, if f = 0 is any line through the common point, then the columns of the matrix

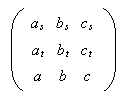
are linearly dependent using the common point, and, since the first two rows are independent, the last row must be a linear combination of the first two. Hence, f = 0 is in the pencil. A similar argument shows that, if f_s = 0 and f_t = 0 are parallel and f = 0 is also parallel, then it is in the pencil: the pencil consists of all lines parallel with the base lines.

2. Change of Base

If

	fu	= su fs + tu ft
	fv	= sv fs + tv ft

give two distinct lines of the pencil, then f_u, f_v can be a new base.

	ufu + vfv	= u(su fs + tu ft) + v(sv fs + tv ft)
		= (usu + vsv)fs + (utu + vtv)ft.

The transition from (u, v) to (s, t) is given by the matrix formula

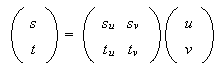
It is important to note that the base is determined by f_s, f_t but not by the lines f_s = 0 and f_t = 0 because, if s_u ≠ t_v the new base f_u = s_u f_s, f_v = t_v f_t has the same base lines with parameters (0, 1), (1, 0) but the other lines get new parameters. To define the base geometrically, a third line, say s_u f_s + t_v f_t = 0 is required and the above change of base gives it parameters (1, 1).

3. Cross-ratio

In terms of the homogeneous parameters for the pencil, the convenient definition of cross-ratio is

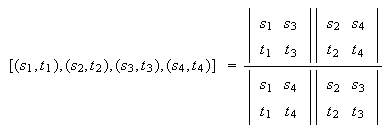
It agrees with the one parameter version if the parameter is replaced by s/t.

Its importance in this context is that it is depends only on the four lines and not on the choice of homogeneous parameters. This becomes obvious using that the determinant of the product of two matrices is the product of the determinants:

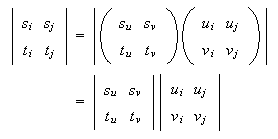
If three different points are given along with the cross-ratio k of them with a forth point, then the forth point is uniquely determined. To prove this, choose the base so that the points have parameters (1, 0), (0, 1), (1, 1), (s, t). By the symmetry properties of cross-ratio they can be assumed to occur in the above order.

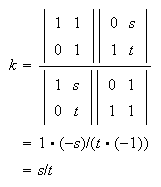
4. Projective Plane

The projective plane is obtained from the ordinary Euclidean plane by adjoining an extra point for each pencil of parallel lines. It is the point 'at infinity' where the lines of the pencil meet. To accommodate the new points it is convenient to introduce homogeneous coordinates. This is done by replacing the usual x, y coordinates with x/z, y/z. Each (x, y, z) ≠ (0, 0, 0) represents a point of the plane but, if r ≠ 0, (rx, ry, rz) represents the same point so the coordinates are homogeneous.

A line in the plane is given by an equation ax + by + cz = 0, where not all of the coefficients are zero. In particular, z = 0 gives the line at infinity and parallel lines

meet at (b, -a, 0) as required.

The line joining points (x_s, y_s, z_s) and (x_t, y_t, z_t) can be described by homogeneous parameters s, t since

s(x_s, y_s, z_s) + t (x_t, y_t, z_t)

is on the line for each (s, t) ≠ (0, 0). If (x₀, y₀, z₀) is a point not on the line, then the equation of the line joining it to the s, t is given by

This can be rewritten

The parameters for the line are the parameters for the pencil of lines through (x₀, y₀, z₀). Therefore the cross-ratio of four points on a line is the same as the cross-ratio of the lines joining a point to them implying that cross-ratio is invariant under projection.

5. Change of Coordinates

The coordinate vectors X = (1, 0, 0), Y = (0, 1, 0), Z = (0, 0, 1) form a base for the coordinate system in the sense that (x, y, z) = xX + yY + zZ. If the points defined by

	X'	= (xx, yx, zx)
	Y'	= (xy, yy, zy)
	Z'	= (xz, yz, zz)

are not collinear, then they can form a new base:

(x, y, z) = x'X' + y'Y' + z'Z'.

In matrix form

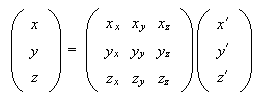
The matrix is invertible since the points are not collinear.

Note that the points defined by X, Y, Z are not sufficient to determine the base because

	X'	= xx X
	Y'	= yy Y
	Z'	= zz Z

defines a new base with the same base points if x_x, y_y, z_z are not all equal. To define a base geometrically, an extra point is needed, say, (x_x, y_y, z_z) which should not be on a line joining two of the other three points. The change of base above then gives this point coordinates (1, 1, 1).

6. Chasles' Theorem

The theorem states that,

for four points on a non-degenerate conic, the cross-ratio of the pencil of four lines from a fifth point of the conic to the given points does not depend on the choice of the fifth point.

To prove this choose a coordinate system such that X and Y are points of the conic, Z is the intersection of the tangents from X and Y and the (1, 1, 1) point is on the conic. The transformation of coordinates is linear and homogeneous so the conic will still be of the form

ax² + by² + cz² + fyz + gxz + hxy = 0.

Since the line y = 0 is tangent at (1, 0, 0), a = g = 0 to give the double root z = 0. Similarly, b = f = 0. Inserting (1, 1, 1) reduces the equation to

xy = z².

Consider the pencil of lines through X with base y, -z. The line with parameters s, t is sy = tz and it meets the conic again at the point (s², t², st). s, t also give a homogeneous parametrization of the conic. Now, consider the pencil through Y with base z, -x. The line sz = tx also meets the conic again at (s², t², st); it gives the same parametrisation of the conic. It follows that the cross-ratios of pencils from X and Y to four points of the conic must be the same. Since X and Y were arbitrary points of the conic, the theorem is true.

(Chasles' theorem leads to an elegant projective proof of Pascal's Theorem. Also, there is another proof of Chasles' Theorem and a third, the simplest of all.)

Chasles' Theorem

• Chasles' Theorem
• Chasles' Theorem, a Simple Proof
• Pascal's Theorem, Homogeneous Coordinates
• Chasles' Theorem, a Proof
• Projective Proof of Pascal's Theorem

|Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny