A Property of Isogonal Lines

What Might This Be About?

Problem

Given angle $BAC,$ line $AP,$ and its reflection in the bisector of $\angle BAC$, say $AP'.$ Let $P_b,$ $P_c$ be the projections of $P$ on the rays $AC$ and $AB,$ respectively.

A Property of Isogonal Lines - problem

Then $P_bP_c \perp AP'.$

Solution

The proof is simple.

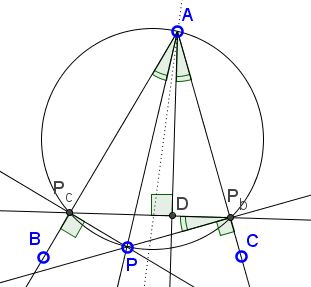
A Property of Isogonal Lines - solution

Let $D$ be the intersection of $AP'$ and $P_bP_c.$ Then quadrilateral $AP_{b}PP_{c}$ is cyclic (and $AP$ is a diameter of its circumcircle.) Now, $\angle PP_{b}P_{c} = \angle PAP_{c}$ as two inscribed angles subtended by the same arc. It is also given that $\angle PAP_{c} = \angle DAP_{b},$ implying $\angle PP_{b}P_{c} = \angle DAP_{b}.$ The latter two angles have one pair of the sides perpendicular, therefore the same holds for the other pair of their sides.

Acknowledgment

References

R. Honsberger, Episodes in Nineteenth and Twentieth Century Euclidean Geometry, MAA, 1995, p. 65
R. A. Johnson, Advanced Euclidean Geometry (Modern Geometry), Dover, 1960, p. 156

72192980