Constant Ratio on Circle
What Is This About?
Problem
Given a circle and on it four points: $U,V,W,P\;$ such that $V$ is the midpoint of an arc $UW\;$ while $P\;$ is arbitrary in the other arc $UW.$
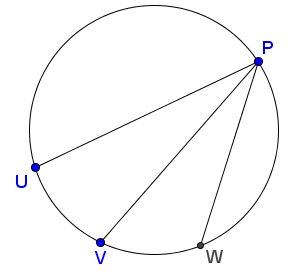
Then the ratio $\displaystyle\frac{PU+PW}{PV}\;$ does not depend on the position of $P.$
Proof
Assume we deal with the unit circle and let $V=(\cos s, \sin s),\;$ $U=(\cos (s-d),\sin (s-d)),\;$ $W=(\cos (s+d),\sin (s+d)),\;$ and $P=(\cos t, \sin t).\;$ Let $M=(\cos m, \sin m)\;$ be a random point on the circle. Then
$\displaystyle\begin{align}MP^2=|M-P|^2&=((\cos m-\cos t)^2+(\sin m-\sin t)^2\\ &=(\cos^2 m+\sin^2m)+(\cos^2t+\sin^2t)-2(\cos m\cos t+\sin m\sin t)\\ &=2-2\cos (m-t)\\ &=4\sin^2\frac{m-t}{2}. \end{align}$
We may assume that $\displaystyle 0\lt\frac{m-v}{2}\lt 180^{\circ},\;$ such that $\displaystyle MP=2\sin\frac{m-t}{2}.$
Using that
$\displaystyle\begin{align} \frac{PU+PW}{PV} &= \frac{\displaystyle 2\sin\frac{s-d-t}{2}+2\sin\frac{s+d-t}{2}}{\displaystyle 2\sin\frac{s-t}{2}}\\ &=\frac{\displaystyle 2\sin\frac{s-t}{2}\cos\frac{d}{2}}{\displaystyle\sin\frac{s-t}{2}}\\ &=2\cos\frac{d}{2}. \end{align}$
Variant
Given a circle and on it six points: $U_2,U_1,V,W_1,W_2,P\;$ such that $V$ is the midpoint of both arcs $U_1W_1\;$ and $U_2W_2\;$ while $P\;$ is arbitrary in the other arc $U_2W_2.$
Then the ratio $\displaystyle\frac{PU_1+PW_1}{PU_2+PW_2}\;$ is independent of position of $P.$
For a proof consider
$\displaystyle\frac{PU_1+PW_1}{PU_2+PW_2}=\frac{PU_1+PW_1}{PV}\cdot\frac{PV}{PU_2+PW_2}$
and apply the previous result.
Acknowledgment
There were two earlier posts: one by Dorin Marghidanu, concerning a constant ratio in a square and another by Dao Thanh Oai, with a comment to the latter by Tim Robinson that suggested a more general, unifying property, as above.
Trigonometry
- What Is Trigonometry?
- Addition and Subtraction Formulas for Sine and Cosine
- The Law of Cosines (Cosine Rule)
- Cosine of 36 degrees
- Tangent of 22.5o - Proof Wthout Words
- Sine and Cosine of 15 Degrees Angle
- Sine, Cosine, and Ptolemy's Theorem
- arctan(1) + arctan(2) + arctan(3) = π
- Trigonometry by Watching
- arctan(1/2) + arctan(1/3) = arctan(1)
- Morley's Miracle
- Napoleon's Theorem
- A Trigonometric Solution to a Difficult Sangaku Problem
- Trigonometric Form of Complex Numbers
- Derivatives of Sine and Cosine
- ΔABC is right iff sin²A + sin²B + sin²C = 2
- Advanced Identities
- Hunting Right Angles
- Point on Bisector in Right Angle
- Trigonometric Identities with Arctangents
- The Concurrency of the Altitudes in a Triangle - Trigonometric Proof
- Butterfly Trigonometry
- Binet's Formula with Cosines
- Another Face and Proof of a Trigonometric Identity
- cos/sin inequality
- On the Intersection of kx and |sin(x)|
- Cevians And Semicircles
- Double and Half Angle Formulas
- A Nice Trig Formula
- Another Golden Ratio in Semicircle
- Leo Giugiuc's Trigonometric Lemma
- Another Property of Points on Incircle
- Much from Little
- The Law of Cosines and the Law of Sines Are Equivalent
- Wonderful Trigonometry In Equilateral Triangle
- A Trigonometric Observation in Right Triangle
- A Quick Proof of cos(pi/7)cos(2.pi/7)cos(3.pi/7)=1/8
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73581311
