Sums of the Elements of Three Element Subsets
Problem
Can one divide the set $\{1,2,\ldots,96\}$ into $32$ subsets of three elements each, such that the sums of the three elements in the subsets are all equal?
Can one divide the set $\{1,2,\ldots,99\}$ into $33$ subsets of three elements each, such that the sums of the three elements in the subsets are all equal?
Hint
To find the answer to the first question think of what that common sum could be. For the second question, try to think what makes the number $99$ is special for this problem. Try to think of perhaps smaller numbers with the same property.
Solution
Solution to #1
The answer is "No", because if, the sums of the elements of the $32$ subsets were equal, then the sum of $1+2+\ldots +96=48\cdot 97$ would be divisible by $32$ which it is clearly not.
Solution to #2
The sum of all integers from $1$ through $99$ is divisible by $33$ so that the argument that worked for the first part of the problem does not work here. Perhaps, this is an indication that the answer to the second part is "Yes"? If so, almost certainly $99$ is not a unique number that could be used in that problem. Trying to find the smallest number that would do the job, I came up with $9:$
$2+6+7=3+4+8=1+5+9=15!$
What made it work? I could observe several properties:
The set $\{1,2,\ldots,9\}$ is the union of three successive subsets ordered by the magnitude of their elements:
$\{1,2,\ldots,9\}=\{1,2,3\}\cup \{4,5,6\}\cup\{7,8,9\}$
such that each of the three sums above contains one and only one element from each of the three subsets.
The elements of the last subset $\{7,8,9\}$ are in arithmetic progression, with $1$ as the difference, suggesting that the union of the two other sets, i.e., $\{1,2,\ldots,6\}$ could be (and were) split into pairs whose sums form an arithmetic progression with $1$ as the difference.
So, had the number of elements in the given set been $9$ and not $99$ the problem would have already been solved. As it is, we have to plough away further on. What other number besides $9$ would work? Obviously, the number needs to be divisible by $3$. Could it be $12?$ No - for exactly same reason $96$ did not work. What about $15?$ There is a chance that it does work. Let's try following in the footsteps of the solution for the $9$-element set:
$\{1,\ldots,15\}=\{1,\ldots,5\}\cup\{6,\ldots,10\}\cup\{11,\ldots,15\}$
If the problem is solvable in this case, the common sums of the three element subsets would be $\displaystyle\frac{15\cdot 16}{2}:5=24.$ Therefore, the task is to form pairs of integers (one from each of the two first subsets) whose sums are in the arithmetic progression:
$24-11=13,\space24-12=12,\ldots,24-15=9.$
The smallest sum in the first example included $1$ so this is where we start: $1+8=9.$ The next smallest sum contained $3$ - try $3+7=10$. Let's continue: $5+6=11,$ $2+10=12,$ and $4+9=13.$ We are done! Here is a solution:
$\begin{align} \{1,2,\ldots,15\} &= \{1,8,15\}\\ & \cup\space\{3,7,14\}\\ & \cup\space\{5,6,13\}\\ & \cup\space\{2,10,12\}\\ & \cup\space\{4,9,11\}, \end{align}$
with the common sum being $24.$ Now, the question is to locate a pattern.
I bet that for the number of elements $3n,$ with $n$ odd the problem is always solvable. Obviously it is not solvable if $n$ is even, as above. The common sum of the three element subsets ought to be $\displaystyle\frac{3n(3n+1)}{2}:n=\frac{3(3n+1)}{2}.$ The three subsets to pick one element from each are
$\{1,\ldots,n\},$ $\{n+1,\ldots,2n\},$ $\{2n+1,\ldots,3n\}.$
We start with $1$ from the first and $3n$ from the third which leaves
$\displaystyle\frac{3(3n+1)}{2}-1-3n=\frac{3n+1}{2}=\frac{(n+1)+2n}{2},$
for the second set. This is exactly its midpoint. The next pick is $3$ from the first set, $\displaystyle\frac{3n+1}{2}-1$ from the second, and $3n-1$ from the third. We can proceed in that manner only till we reach $n$ in the first set. This will correspond to $n+1$ in the second, and $\displaystyle 3n-\frac{n-1}{2}=\frac{5n+1}{2}=(2n+1)+\frac{n-1}{2}$ from the third. From here we start with $2$ from the first set, $2n$ from the second, and $\displaystyle \frac{5n+1}{2}-1$ from the third. You can check that this process will carry us through.
Coming back to the original problem of $n=33,$ the following is the answer:
$\begin{align} 150 &= 1+50+99 \\ &= 3+49+98 \\ &\dots \\ &= 31 + 35 + 84\\ &= 33 + 34 + 83\\ &= 2 + 66 + 82\\ &= 4 + 65 + 81\\ &\dots \\ &= 30 + 52 + 68\\ &= 32 + 51 + 67. \end{align}$
More solutions
Yuriy Kazakov found three more solutions and summarized all four in the following table:
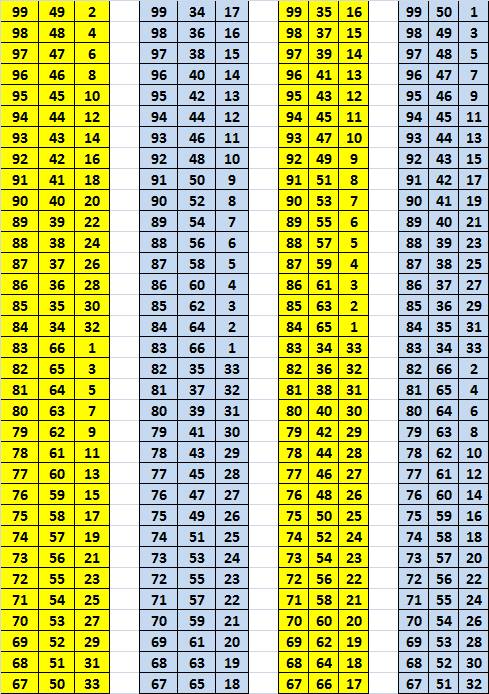
Acknowledgment
This is a problem from the 2008 China Girl's Mathematical Olympiad [Xiong Bin, pp 94-96].
References
- Xiong Bin, Lee Peng Yee, Mathematical Olympiads in China (2009-2010). Problems and Solutions, World Scientific, 2013
Trigonometry
- What Is Trigonometry?
- Addition and Subtraction Formulas for Sine and Cosine
- The Law of Cosines (Cosine Rule)
- Cosine of 36 degrees
- Tangent of 22.5o - Proof Wthout Words
- Sine and Cosine of 15 Degrees Angle
- Sine, Cosine, and Ptolemy's Theorem
- arctan(1) + arctan(2) + arctan(3) = π
- Trigonometry by Watching
- arctan(1/2) + arctan(1/3) = arctan(1)
- Morley's Miracle
- Napoleon's Theorem
- A Trigonometric Solution to a Difficult Sangaku Problem
- Trigonometric Form of Complex Numbers
- Derivatives of Sine and Cosine
- ΔABC is right iff sin²A + sin²B + sin²C = 2
- Advanced Identities
- Hunting Right Angles
- Point on Bisector in Right Angle
- Trigonometric Identities with Arctangents
- The Concurrency of the Altitudes in a Triangle - Trigonometric Proof
- Butterfly Trigonometry
- Binet's Formula with Cosines
- Another Face and Proof of a Trigonometric Identity
- cos/sin inequality
- On the Intersection of kx and |sin(x)|
- Cevians And Semicircles
- Double and Half Angle Formulas
- A Nice Trig Formula
- Another Golden Ratio in Semicircle
- Leo Giugiuc's Trigonometric Lemma
- Another Property of Points on Incircle
- Much from Little
- The Law of Cosines and the Law of Sines Are Equivalent
- Wonderful Trigonometry In Equilateral Triangle
- A Trigonometric Observation in Right Triangle
- A Quick Proof of cos(pi/7)cos(2.pi/7)cos(3.pi/7)=1/8
![]()
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73518718
