Arctan Identity and its Consequence
What Is This About?
18 May 2016, Created with GeoGebra
Explanation
Assume in a right $\Delta BCD,\;$ $AC\perp BD,\;$ with $A,E,F\;$ on $BC\;$ such that $DE=AB\;$ and $EF=AF.\;$ Then $\angle AFC=2\angle ACB.$
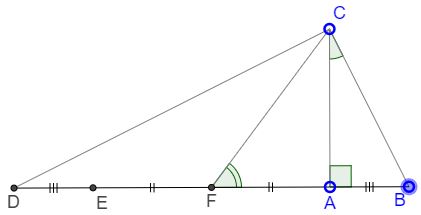
Statement
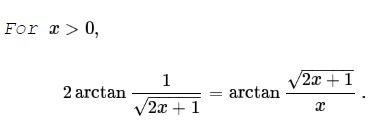
Proof 1
As is well known, $\displaystyle \tan 2\alpha=\frac{2\tan\alpha}{1-\tan^2\alpha}.\;$ Using that and $\tan(\arctan\alpha)=\alpha,$
$\displaystyle\begin{align} \tan\left( 2\arctan\frac{1}{\sqrt{2x+1}}\right)&=\frac{\displaystyle\frac{2}{\sqrt{2x+1}}}{\displaystyle 1-\left(\frac{1}{\sqrt{2x+1}}\right)^2}\\ &=\frac{\displaystyle\frac{2}{\sqrt{2x+1}}}{\displaystyle \frac{2x}{2x+1}}\\ &=\frac{\sqrt{2x+1}}{x}. \end{align}$
This proves the statement which can be rewritten as
$\displaystyle\frac{\displaystyle\arctan\frac{1}{\sqrt{2x+1}}}{\displaystyle\arctan\frac{\sqrt{2x+1}}{x}}=\frac{1}{2}.$
Proof 2
Define $\displaystyle f(x)=2\arctan\frac{1}{\sqrt{2x+1}}\;$ and $\displaystyle g(x)=\arctan\frac{\sqrt{2x+1}}{x}.\;$ Then
$\displaystyle f'(x)=-\frac{1}{\sqrt{2x+1}(x+1)},\\ \displaystyle g'(x)=-\frac{1}{\sqrt{2x+1}(x+1)}.$
It follows that $f(x)-g(x)=\mbox{const}.\;$ But $\displaystyle f(1)=2\arctan\left(\frac{1}{\sqrt{3}}\right)=2\cdot\frac{\pi}{6},\;$ while $\displaystyle g(1)=\arctan\sqrt{3}=\frac{\pi}{3}.\;$ Hence $f(x)=g(x).$
Corollary
$\displaystyle\sum_{k=1}^n\frac{\displaystyle\arctan\frac{1}{\sqrt{2k+1}}}{\displaystyle\arctan\frac{\sqrt{2k+1}}{k}}=\frac{n}{2}.$
Acknowledgment
What I made as Corollary has been posted by Rovshan Pirkuliev at the Imad Zak Math facebook page. Proof 1, based on the Statement above, is due to Ghimisi Dumitrel. Proof 2 is by Imad Zak. The applet at the top of the page is just an illustration of the underlying trigonometric identity. This is certainly not the most efficient way to double an angle.
Trigonometry
- What Is Trigonometry?
- Addition and Subtraction Formulas for Sine and Cosine
- The Law of Cosines (Cosine Rule)
- Cosine of 36 degrees
- Tangent of 22.5o - Proof Wthout Words
- Sine and Cosine of 15 Degrees Angle
- Sine, Cosine, and Ptolemy's Theorem
- arctan(1) + arctan(2) + arctan(3) = π
- Trigonometry by Watching
- arctan(1/2) + arctan(1/3) = arctan(1)
- Morley's Miracle
- Napoleon's Theorem
- A Trigonometric Solution to a Difficult Sangaku Problem
- Trigonometric Form of Complex Numbers
- Derivatives of Sine and Cosine
- ΔABC is right iff sin²A + sin²B + sin²C = 2
- Advanced Identities
- Hunting Right Angles
- Point on Bisector in Right Angle
- Trigonometric Identities with Arctangents
- The Concurrency of the Altitudes in a Triangle - Trigonometric Proof
- Butterfly Trigonometry
- Binet's Formula with Cosines
- Another Face and Proof of a Trigonometric Identity
- cos/sin inequality
- On the Intersection of kx and |sin(x)|
- Cevians And Semicircles
- Double and Half Angle Formulas
- A Nice Trig Formula
- Another Golden Ratio in Semicircle
- Leo Giugiuc's Trigonometric Lemma
- Another Property of Points on Incircle
- Much from Little
- The Law of Cosines and the Law of Sines Are Equivalent
- Wonderful Trigonometry In Equilateral Triangle
- A Trigonometric Observation in Right Triangle
- A Quick Proof of cos(pi/7)cos(2.pi/7)cos(3.pi/7)=1/8
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73615439
