Hadamard's Determinant Inequalities and Applications I
Problem
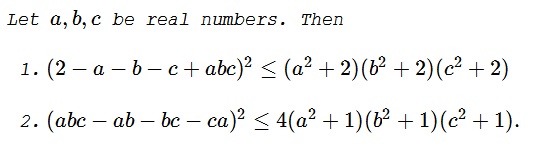
Hadamard's First Theorem
If $A=(a_{ij})\in M_n(\mathbb{R}),$ then
$\displaystyle (\det A)^2\le\prod_{j=1}^n\left(\sum_{i=1}^na_{ij}^2\right).$
(See, e.g., Hadamard's theorem on determinants.)
Problem 1, Solution
Consider a $3\times 3$ matrix $A=\left(\begin{array}{ccc}a&1&1\\1&b&1\\1&1&c\end{array}\right).$ One can verify that $\det A=2-a-b-c+abc.$ Thus, the required inequality is a direct consequence of Hadamard's First Theorem.
Problem 2, Solution
Consider a $4\times 4$ matrix $A=\left(\begin{array}{ccc}1&1&1&1\\1&a&0&0\\1&0&b&0\\1&0&0&c\end{array}\right).$ One can verify that $\det A=abc-a-b-c.$ Thus, the required inequality is a direct consequence of Hadamard's First Theorem.
Acknowledgment
The above is based on an article Application of Hadamard's Theorems to inequalities by Dan Sitaru and Leo Giugiuc that appeared in the Crux Mathematicorum (v 44, n 1, pp 25-27). I am very much indebted to Dan Sitaru for bringing this article to my attention.
Related material
| |
Linear Algebra Tools for Proving Inequalities$\;\left(\displaystyle\left(\frac{a}{b-c}\right)^2+\left(\frac{b}{c-a}\right)^2+\left(\frac{c}{a-b}\right)^2\ge 2\right)$ | |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
![]()
Cyclic inequalities in three variables
- ab + bc + ca does not exceed aa + bb + cc
- A Cyclic Inequality in Three Variables $\left(\displaystyle\frac{a^3}{b^2(5a+2b)}+\frac{b^3}{c^2(5b+2c)}+\frac{c^3}{a^2(5c+2a)}\ge\frac{3}{7}\right)$
- A Cyclic Inequality in Three Variables II $\left(\displaystyle\frac{10a^3}{3a^2+7bc}+\frac{10b^3}{3b^2+7ca}+\frac{10c^3}{3a^2+7ab}\ge a+b+c\right)$
- A Cyclic Inequality in Three Variables III $\left(\displaystyle\sqrt{\frac{a}{b+c}}+\sqrt{\frac{b}{c+a}}+\sqrt{\frac{c}{a+b}}\ge 2\right)$
- A Cyclic Inequality in Three Variables IV $\left(\displaystyle 2\sum_{cycl}(a+b)^3+5\sum_{cycl}a^3\ge 21\sum_{cycl}a^2b\right)$
- A Cyclic Inequality in Three Variables V $\left(\displaystyle \frac{a}{b}+\frac{b}{c}+\frac{c}{a}\ge\frac{\sqrt{3(a^2+b^2+c^2)}\cdot (a+b+c)}{ab+bc+ca}\right)$
- A Cyclic Inequality in Three Variables VI $\left(\displaystyle \frac{2(a+b+c)}{abc}\ge\sum_{cycl}\left(\sqrt{\frac{a+b}{2ac}}+\sqrt{\frac{2a}{c(a+b)}}\right)\right)$
- A Cyclic Inequality in Three Variables VII $\left(\displaystyle\sum_{cycl}x\sqrt{x^2z^2+y^4}\ge\sqrt{2}\sum_{cycl}xz\sqrt{yz}\right)$
- A Cyclic Inequality in Three Variables VIII $\left(\displaystyle\sum_{cycl}(x^2+y^2)z+\sum_{cycl}\frac{xy}{(x+y)^2}\ge 27xyz\right)$
- A Cyclic Inequality in Three Variables IX $\left(\displaystyle 9\left(\sum_{cycl}\frac{x^2}{y^2}\right)^2\ge 8\left(\sum_{cycl}\frac{x}{y}\right)\left(\sum_{cycl}\frac{x^3}{y^3}-3\right)\right)$
- A Cyclic Inequality in Three Variables X $\left(\displaystyle\sum_{cycl}\frac{1}{(a+1)^3}+4\sum_{cycl}\frac{1}{(a+1)^4}\ge\frac{9}{8}\right)$
- A Cyclic Inequality in Three Variables XI $\left(\displaystyle\sum_{cycl}\frac{1}{(a^2-ab+b^2)(b^2-bc+c^2)}\le\sum_{cycl}\frac{1}{a^4}\right)$
- A Cyclic Inequality in Three Variables XII $\left(\displaystyle\left(\sum_{cycl}\frac{1}{(a^2-ab+b^2)^6}\right)^2\le 3\sum_{cycl}\left(\frac{a+b}{a^2+b^2}\right)^{24}\right)$
- A Cyclic Inequality in Three Variables XIII $\left(\displaystyle\sum_{cycl}\frac{a^2+b^2}{a+b}+11\sum_{cycl}\frac{ab}{a+b}\gt 6\sum_{cycl}\sqrt{ab}\right)$
- A Cyclic Inequality in Three Variables XIV $\left(\displaystyle\sum_{cycl}\frac{xy}{xy+y^2+zx}\le 1\right)$
- A Cyclic Inequality in Three Variables XV $\left(\displaystyle \frac{a(a^2+b^2)}{a^3+b^3}+\frac{b(b^2+c^2)}{b^3+c^3}+\frac{c(c^2+a^2)}{c^3+a^3}\leq \sqrt{\frac{a}{b}}+\sqrt{\frac{b}{c}}+\sqrt{\frac{c}{a}}\right)$
- A Cyclic Inequality in Three Variables XVI $\left(\displaystyle \sum_{cycl}|(a+b)(1-ab)|\lt\frac{3}{2}+\sum_{cycl}a^2+\frac{1}{2}\sum_{cycl}a^4\right)$
- A Cyclic Inequality in Three Variables XVII $\left(\displaystyle \left(\sum_{cycl}\frac{x^2}{y^2}\right)^5 \ge 9\left(\sum_{cycl}\frac{x^3}{y^2z}\right)\left(\sum_{cycl}\frac{x}{\sqrt{yz}}\right)\left(\sum_{cycl}\frac{y}{z}\right)\right)$
- A Cyclic Inequality in Three Variables XVIII $\left(\displaystyle \left(\sum_{cycl}\sqrt{ab}\right)^6 \le 27\prod_{cycl}(a^2+ab+b^2)\right)$
- A Cyclic Inequality in Three Variables XIX $\left(\displaystyle \frac{x}{(y+z)^3}+\frac{y}{(z+x)^3}+\frac{z}{(x+y)^3}\ge\frac{27}{8(x+y+z)^2}\right)$
- A Cyclic Inequality in Three Variables XX $\left(\displaystyle 5\sum_{cycl}\sqrt{ab}\le\sum_{cycl}\sqrt[4]{(a+4b)(2a+3b)(3b+2a)(4a+b)}\le 5\right)$
- A Cyclic Inequality in Three Variables XXI $\left(\displaystyle \frac{abc}{7\sqrt{7}}\le\prod_{cycl}\frac{a^2-ab+b^2}{\sqrt{a^2+5ab+b^2}}\right)$
- A Cyclic Inequality in Three Variables XXII $\left(\displaystyle \sum_{cycl}\frac{a^3}{a^2+ab+b^2}\ge\frac{a+b+c}{3}\right)$
- A Cyclic Inequality in Three Variables XXIII $\left(\displaystyle 3(a^2+b^2+c^2)^2\ge 8abc(a+b+c)+\sum_{cycl}(a^2+b^2-c^2)^2\right)$
- A Cyclic Inequality in Three Variables XXIV $\left(\displaystyle \sum_{cycl} \frac{a^2b^2 (1+a^2)(1+b^2)}{(1+a)(1+b)}\geq 4(3-2\sqrt{2})abc(a+b+c)\right)$
- A Cyclic Inequality in Three Variables XXV $\left(\displaystyle \sum_{cycl} (a-\sqrt{ab}+b)^2\cdot\sum_{cycl}(a^2-ab+b^2)^2\ge 9a^2b^2c^2\right)$
- A Cyclic Inequality in Three Variables And One More $\left(\displaystyle \left(\sum_{cycl}x^{2m+2}\right)\cdot\left(\sum_{cycl}\frac{1}{(x+y)^{2m+2}}\right)\ge\frac{9}{4^{m+1}}\right)$
- Dorin Marghidanu's Cyclic Inequality in Three Variables $\left(\displaystyle\sum_{cycl}\sqrt{a^2-ab+b^2}\sqrt{b^2-bc+c^2}\ge a^2+b^2+c^2\right)$
- Dorin Marghidanu's Cyclic Inequality in Three Variables II
$\left(\displaystyle\sum_{cycl}\frac{ab}{(a+c)(b+c)} \ge\frac{3}{4}\right)$
Dorin Marghidanu's Cyclic Inequality in Three Variables III
$\left(\displaystyle \frac{a^3}{b^2+c}+\frac{b^3}{c^2+a}+\frac{c^3}{a^2+b}\gt \frac{3}{2}(abc)^{\frac{2}{3}}\right)$
- Leo Giugiuc's Cyclic Inequality in Three Variables $\left(\displaystyle a^2+b^2+c^2\ge 3\sqrt[3]{\frac{1}{4}(a-b)^2(b-c)^2(c-a)^2}+ab+bc+ca\right)$
- Tran Hoang Nam's Cyclic Inequality in Three Variables $\left(\displaystyle\sum_{cycl}(a-b)^3(a-c)^3 \le \left(\sum_{cycl}a^2-\sum_{cycl}ab\right)^3\right)$
- Cyclic Inequality with Square Roots $\left(\displaystyle 2\sqrt{2}\sum_{cycl}xy\ge\sqrt{2xyz}\sum_{cycl}\sqrt{x}+\sum_{cycl}\sqrt{x^2z^2+y^2z^2}\right)$
- Cyclic Inequality with Logarithms $\left(\displaystyle \ln \left(a^b\cdot b^c\cdot c^a\right)+6\sum_{cycl}\frac{b(1+2a)}{1+4a+a^2}\ge 3(a+b+c)\right)$
- A Cyclic Inequality with Many Sums $\left(\displaystyle\small{ \left(\sum_{cycl}a^4\right)\left(\sum_{cycl}\frac{a}{b}\right)\left(\sum_{cycl}a^3\right)\left(\sum_{cycl}\frac{a}{c}\right)\left(\sum_{cycl}a^2\right) \ge \left(\sum_{cycl}a\right)^3\left(\sum_{cycl}\frac{1}{a}\right)^2}\right)$
- Dan Sitaru's Cyclic Inequality in Three Variables III $\left(\displaystyle 4\sqrt{\sum_{cycl}\frac{a}{(a-1)^2}}\ge\sqrt{6}(10-a-b-c)\right)$
- Imad Zak's Cyclic Inequality in Three Variables $\left(\displaystyle \frac{(a+b+c)^2}{ab+bc+ca} + \frac{ab+bc+ca}{a^2+b^2+c^2}\ge 4\right)$
- Imad Zak's Cyclic Inequality in Three Variables II $\left(\displaystyle \frac{ab+bc+ca}{(a+b+c)^2} + \frac{a^2+b^2+c^2}{ab+bc+ca}\ge \frac{4}{3}\right)$
- A Simple Cyclic Inequality in Three Variables $\left(\displaystyle 3\left(\sum_{cycl}a^2\right)^2\ge 8abc(a+b+c)+\sum_{cycl}(a^2+b^2-c^2)^2\right)$
- An Inequality with Cyclic Sums on Both Sides $\left(\displaystyle \sum_{cycl}\frac{a^9}{b^6c^2}\ge\sum_{cycl}\sqrt[6]{\frac{a^{28}}{b^{17}c^5}}\right)$
- An Inequality with Cyclic Sums on Both Sides II $\left(\displaystyle \sum_{cycl}\sqrt[6]{ab^2c^3}\ge\sum_{cycl}\sqrt[30]{a^{9}b^{10}c^{11}}\right)$
- An Inequality with Cyclic Sums on Both Sides III $\left(\displaystyle \frac{x^6z^3+y^6x^3+z^6y^3}{x^2y^2z^2}\geq \frac{x^3+y^3+z^3+3xyz}{2}\right)$
- A Cyclic Inequality in Three Variables with a Variable Hierarchy $\left(\displaystyle 2(x^2y + y^2z + z^2x+xyz) \ge (x+y) (y+z) (z+x)\right)$
- Dan Sitaru's Cyclic Inequality In Three Variables $\left(\displaystyle \frac{(5a+b)(5b+c)(5c+a)}{27(a+8c)(b+8a)(c+8b)}\geq \frac{8abc}{(5a+4b)(5b+4c)(5c+a)}\right)$
- Dan Sitaru's Cyclic Inequality in Three Variables V $\left(\displaystyle (x+y+z)^2\le \sum_{cycl}\sqrt{(x^2+xy+y^2)(y^2+yz+z^2)}\right)$
- Dan Sitaru's Cyclic Inequality in Three Variables VII $\left(\displaystyle \frac{5x+3y+z}{5z+3y+x}+\frac{5y+3z+x}{5x+3z+y}+\frac{5z+3x+y}{5y+3x+z}\ge 3\right)$
- Problem 11867 from the American Mathematical Monthly $\displaystyle \left(\left(\frac{a^2}{a^2-ab+b^2}\right)^{\frac{1}{4}} + \left(\frac{b^2}{b^2-bc+c^2}\right)^{\frac{1}{4}} + \left(\frac{c^2}{c^2-ca+a^2}\right)^{\frac{1}{4}} \le 3\right)$
- An Inequality from the 1967 IMO Shortlist $\left(\displaystyle \frac{1}{a}+\frac{1}{b}+\frac{1}{c}\le\frac{a^8+b^8+c^8}{a^3b^3c^3}\right)$
- Birth of an Inequality $\displaystyle\left(3(a^2+b^2+c^2)^2\ge 24abc\sqrt[3]{abc}+\sum_{cyc}(a^2+b^2-c^2)^2\right)$
- A Simple Inequality in Three Variables $\displaystyle\left(\sum_{cyc}ac\left(\frac{1}{2a+b}+\frac{1}{2c+b}\right)\le \sqrt{3(a^2+b^2+c^2)}\right)$
- Cyclic Inequality in Three Variables by Marian Cucoanes $\displaystyle\left( \prod_{cycl}(\sqrt{(a+b)(a+c)}-\sqrt{bc})\ge abc\right)$
- Hung Viet's Inequality IV $\left(\displaystyle \sum_{cycl}\frac{1}{a+5b}\ge\sum_{cycl}\frac{1}{a+2b+3c}\right)$
- Cyclic Inequality with Arctangents $\left(\displaystyle 4\sum_{cycl}ab\cdot\arctan\frac{c}{b}\le\pi\sum_{cycl}a^2\right)$
- A Cyclic Inequality with Powers 2 through 7 $\left(\displaystyle \sum_{cycl}\frac{(a^7+b^7)^3}{(a^4+b^4)(a^5+b^5)(a^6+b^6)}\ge 3a^2b^2c^2\right)$
- A Long Cyclic Inequality of Degree 4 $\left(\displaystyle 4\cdot\sum_{cycl}ab\cdot\sum_{cycl}a-\left(\sum_{cycl}a\right)^3\ge\frac{\displaystyle 3\sum_{cycl}ab\left[4\sum_{cycl}ab-\left(\sum_{cycl}a\right)^2\right]}{\displaystyle \sum_{cycl}a}\right)$
- A Cyclic Inequality from the 6th IMO, 1964 $\left(\displaystyle \sum_{cycl}a^2(b+c-a)\le 3abc\right)$
- Inequality from Math Phenomenon $\left(\displaystyle \frac{a^{2n+1}}{\sqrt{bc}}+\frac{b^{2n+1}}{\sqrt{ac}}+\frac{c^{2n+1}}{\sqrt{ab}}\ge a^{2n}+b^{2n}+c^{2n}\right)$
- A Cyclic Inequality from Math Phenomenon $\left(\displaystyle \frac{1}{a(b+c)}+\frac{1}{b(c+a)}+\frac{1}{c(a+b)}\ge\frac{12}{(a+b+c)^2}\right)$
- Trigonometric Inequality with Integrals $\left(\small{\Omega(a,b)+\Omega(b,c)+\Omega(c,a)\le \sqrt{2}(a^2+b^2+c^2),\;\Omega(a,b)=\int_a^{2a}\int_b^{2b}|\sin (x-y)\cos (x+y)-\sin (x+y)|dxdy}\right)$
- A Cyclic Inequality in Three Variables by Uche E. Okeke $\left(\displaystyle \frac{(a+b)(b+c)(c+a)}{2}\ge abc+ \frac{(ab+bc+ca)^2}{a+b+c}\right)$
- Problem 4142 From Crux Mathematicorum $\displaystyle\left(\Bigr(1+\frac{a^2+b^2+c^2}{ab+bc+ca}\Bigr)^{\frac{(a+b+c)^2}{a^2+b^2+c^2}}\leq \Bigr(1+\frac{a}{b}\Bigr)\Bigr(1+\frac{b}{c}\Bigr)\Bigr(1+\frac{c}{a}\Bigr)\right)$
- Two-Sided Inequality by Dorin Marghidanu $\left(\displaystyle \sqrt{2}\le\sum_{cycl}\frac{b+c}{a+\sqrt{2(b^2+c^2)}}\le 2\right)$
- A Cyclic Inequality In Three Variables by Sorin Radulescu $\left(\displaystyle \left[\sum_{cycl}x(y-z)^2\right]^3\ge 54\prod_{cycl}x(y-z)^2\right)$
- Problem 1 from the 2017 Canada MO $\left(\displaystyle\left(\frac{a}{b-c}\right)^2+\left(\frac{b}{c-a}\right)^2+\left(\frac{c}{a-b}\right)^2\gt 2\right)$
- An Easy Cyclic Inequality And a Remark $\left(\displaystyle 1\le\frac{a}{a+b}+\frac{b}{b+c}+\frac{c}{c+a}\le 2\right)$
- A Cyclic Inequality from India In Three Variables And More $\left(\displaystyle \sum_{cycl}\sqrt{a^4+a^2b^2+b^4}+(6-\sqrt{3})\sum_{cycl}ab\ge 2\left(\sum_{cycl}a\right)^2\right)$
- Dan Sitaru's Cyclic Inequality in Three Variables VIII $\left(\displaystyle (xy+yz+zx)\sum_{cycl}\sqrt{x^2+xy+y^2}\le 3\sqrt{\prod_{cycl}(x^2+xy+y^2)}\right)$
- Hadamard's Determinant Inequalities and Applications I
- An Inequality with Two Triples of Variables II $\left(\displaystyle\small{ ax+by+cz+\sqrt{\left(\sum_{cycl}a^2\right)\left(\sum_{cycl}x^2\right)}\ge\frac{2}{3}\left(\sum_{cycl}a\right)\left(\sum_{cycl}x\right)}\right)$
- Two Cyclic Inequalities $\left(\displaystyle \frac{1}{a(1+b)}+\frac{1}{b(1+c)}+\frac{1}{c(1+a)}\ge\frac{3}{1+abc}\right),$ $\left(\begin{align} \displaystyle 3+(A+M+S)+\bigg(\frac{1}{A}+\frac{1}{M}+\frac{1}{S}\bigg)&+\bigg(\frac{A}{M}+\frac{M}{S}+\frac{S}{A}\bigg)\\&\ge\frac{3(A+1)(M+1)(S+1)}{AMS+1}\end{align}\right)$
- Ji Chen's Inequality $\left(\displaystyle (xy+yz+zx)\left(\frac{1}{(x+y)^2}+\frac{1}{(y+z)^2}+\frac{1}{(z+x)^2}\right)\ge\frac{9}{4}\right)$
- A Cyclic Inequality of Degree Four $\left(\displaystyle a^4b+b^4c+c^4a+2(a+b+c)\ge \sqrt{3}(ab+bc+ca)\right)$
- A Little More of Algebra for an Inequality, A Little Less of Calculus for a Generalization $\left(\displaystyle \sum_{cycl}(a-b)\cdot\left(\frac{a}{b}\right)^n\ge \sum_{cycl}(a-b)\cdot\frac{a}{b}\right)$
- A Cyclic Inequality in Three Variables XXVI $\left(\displaystyle \sum_{cycl}\frac{(x+y)^4+1}{(x+y)^6+1}\le\frac{1}{2}\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)\right)$
- Dorin Marghidanu's Inequality with Powers and Reciprocals $\left(\displaystyle \sum_{cycl}\frac{a}{a^2bc+b^4+c^4}\le\frac{1}{abc}\right)$
![]()
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73582511
