Hadamard's Determinant Inequalities and Applications II
Problem
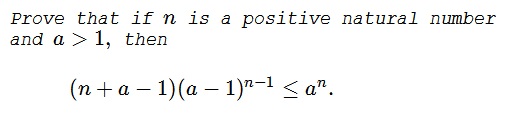
Hadamard's Second Theorem
A square matrix $A=(a_{ij})$ is said to be positive if, for all $i=1,2,\ldots,n,$ $a_{ii}\ge 0$ and $\det A\ge 0.$
If $A=(a_{ij})\in M_n(\mathbb{R})$ is positive, then
$\displaystyle \det A\le\prod_{j=1}^na_{ii}.$
(E.g., Finbarr Holland, Another Proof of Hadamard's Determinantal Inequality, Irish Math. Soc. Bulletin 59 (2007), 61-64)
Solution 1
Consider the $n\times n$ matrix $\displaystyle M_n=\left(\begin{array}{ccccc}a&1&1&\cdots&1\\1&a&1&\cdots&1\\\vdots&\vdots&\vdots&\ddots&\vdots\\1&1&1&\cdots&a\end{array}\right).$
We are going to prove that $\det M_n=(n + a - 1)(a - 1)^{n-1},$ which immediately implies the required inequality. The proof is by induction by induction.
Let's denote $\det M_n=D_n$ and $\displaystyle N_n=\left(\begin{array}{ccccc}1&1&1&\cdots&1\\1&a&1&\cdots&1\\\vdots&\vdots&\vdots&\ddots&\vdots\\1&1&1&\cdots&a\end{array}\right).$
By subtracting the first row from the rest $\det N_n=(a-1)^{n-1}.$ Further, $D_2=a^2-1=(a+2-1)(a-1)^{2-1}.$ Assume that indeed $D_n=(a+n-1)(a-1)^{n-1}.$ Then, by expanding along the first column and swapping the columns to reduce several determinants to one,
$\begin{align}D_{n+1}&=aD_n-n\det N_n=a(a+n-1)(a-1)^{n-1}-n(a-1)^{n-1}\\ &=(a-1)^{n-1}(a^2+an-a-n)\\ &=(a-1)^{n-1}(a(a+n)-(a+n))\\ &=(a-1)^{n}(a+n)\\ &=(a+(n+1)-1)(a-1)^{(n+1)-1}, \end{align}$
as required.
Solution 2
Let $b=a-1.$ Then the required inequality reduces to $(b+1)^n\ge b^{n-1}(n+b)=b^n+nb^{n-1},$ which is obviously true since the right-hand side is just a part of the binomial expansion of $(b+1)^n.$
Acknowledgment
The above is based on an article Application of Hadamard's Theorems to inequalities by Dan Sitaru and Leo Giugiuc that appeared in the Crux Mathematicorum (v 44, n 1, pp 25-27). I am very much indebted to Dan Sitaru for bringing this article to my attention.
Related material
| |
Linear Algebra Tools for Proving Inequalities$\;\left(\displaystyle\left(\frac{a}{b-c}\right)^2+\left(\frac{b}{c-a}\right)^2+\left(\frac{c}{a-b}\right)^2\ge 2\right)$ | |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
![]()
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73582060
