A Cyclic Inequality in Three Variables XIX
Problem
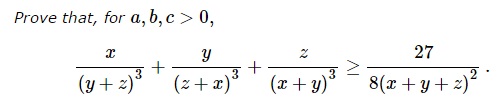
Solution 1
Since the inequality is homogeneous we may assume $x+y+z=3.\,$ It then becomes:
$\displaystyle \frac{x}{(3-x)^3}+\frac{y}{(3-y)^3}+\frac{z}{(3-z)^3}\ge\frac{3}{8},$
$0\le x,y,z\le 3.\,$ Verify that
$\displaystyle\frac{x}{(3-x)^3}-\left(\frac{15x}{16}-\frac{3}{16}\right)=\frac{(x-1)^2(5x^2-38x+81)}{16(3-x)^3}\ge 0.$
Thus
$\displaystyle \begin{align} \sum_{cycl}\frac{x}{(3-x)^3}&\ge\sum_{cycl}\frac{5x}{16}-\sum_{cycl}\frac{3}{16}\\ &=\frac{5(x+y+z)}{16}-\frac{9}{16}=\frac{6}{16}=\frac{3}{8}. \end{align}$
Equality only when $x=y=z=1.$
Solution 2
We'll start with Radon's inequality:
$\displaystyle \begin{align} \sum_{cycl}\frac{x}{(y+z)^3} &= \sum_{cycl}\frac{x^4}{[x(y+z)]^3}\\ &\ge \frac{(x+y+z)^4}{[2(xy+yz+zx)]^3}. \end{align}$
Therefore, suffice it to prove that $\displaystyle\frac{(x+y+z)^4}{(xy+yz+zx)^3}\ge\frac{27}{(x+y+z)^2},\,$ which is equivalent to
$(x+y+z)^2\ge 3(xy+yz+zx),$
This, in turn, is equivalent to $x^2+y^2+z^2\ge xy+yz+zx\;$ and is proved by, say, rearranegment.
Acknowledgment
This is problem SP053 from the Spring 2017 issue of the Romanian Mathematical Magazine, posted by D. M. Batinetu (Romania.) Solution 1 is by Imad Zak (Lebanon).
![]()
|Contact| |Up| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73554064
