A Cyclic Inequality in Three Variables XIII
Problem
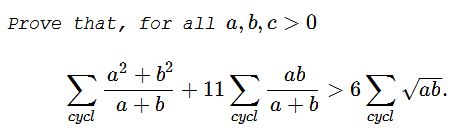
Solution 1
The inequality is equivalent to
$\displaystyle\sum_{cycl}\frac{(a+b)^2+9ab-6(a+b)\sqrt{ab}}{a+b}\gt 0.$
This simplifies to $\displaystyle\sum_{cycl}\frac{(a+b-3\sqrt{ab})^2}{a+b}\gt 0,\,$ which is obvious.
Solution 2
Using the AM-GM inequality,
$\displaystyle\frac{a^2+b^2}{a+b}+\frac{11ab}{a+b}=\frac{(a+b)^2}{a+b}+\frac{9ab}{a+b}\ge 6\sqrt{ab}$
and similar for the other terms.
Solution 3
Set $a+b=s,\,$ $ab=r.\,$ The required inequality becomes
$s^2-6s\sqrt{r}+r\gt 0.$
Since $(s^2-6s\sqrt{r}+r=(s-3\sqrt{r})^2\ge 0.\,$ we only need to show that the equality is not possible. The equality would mean $s-3\sqrt{r}=0,\,$ i.e., $a+b=3\sqrt{ab},\;$ or, $\displaystyle \sqrt{a}=\frac{\sqrt{b}(7\pm 3\sqrt{5})}{2}.\,$ Similarly, $\displaystyle \sqrt{b}=\frac{\sqrt{c}(7\pm 3\sqrt{5})}{2}\,$ and $\displaystyle \sqrt{c}=\frac{\sqrt{a}(7\pm 3\sqrt{5})}{2}.\,$ The product of the three equates a rational number $1\,$ to an irrational number $\displaystyle\left(\frac{7\pm 3\sqrt{5}}{2}\right)^3\,$ which is impossible. Thus, the required inequality is indeed strict.
Acknowledgment
Dan Sitaru has kindly posted the above problem (from his book "Math Accent") at the CutTheKnotMath facebook page, with solutions by Diego Alvariz, Ravi Prakash (India, Solution 1), Seyran Ibrahimov (Azerbaijan, Solution 2), Mihalcea Andrei Stefan (Romania) and Abdallah El Farissi (Algeria) Solution 3.
![]()
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73562807
