An Inequality from Gazeta Matematica, March 2016 IV
Problem
Several inequalities with solution by Dan Sitaru and Leo Giugiuc have been just published in Gazeta Matematica (March 2016). Here is one of two exercises that lets you check your understanding of the technique. I have.
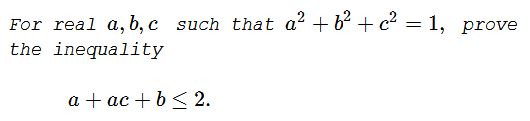
Proof 1
Define $A=\left(\begin{array}\;a&b&c\\1&1&a\end{array}\right).$ By the Binet-Cauchy theorem, $\det(AA^T)\ge 0.\;$ But
$\det(AA^T)=(a^2+b^2+c^2)(2+a^2)-(a+ac+b)^2\ge 0,$
which is $2+a^2\ge (a+ac+b)^2.\;$ Given that $a^2\le a^2+b^2+c^2=1,\;$ we conclude that
$3\ge 2+a^2\ge (a+ac+b)^2,$
i.e., $a+ac+b\le\sqrt{3}\;$ - a somewhat stronger inequality than is required.
With the constraint $a^2+b^2+c^2=2,\;$ we are led to $4\ge 2+a^2\ge (a+ac+b)^2,\;$ and $a+ac+b\le 2.\;$ Ought to be a typo.
Proof 2
The proof which is due to Redwane El Mellass has been posted at the CutTheKnotMath facebook page by Dan Sitaru.
For $\alpha,\beta,\gamma\in [-1,1],\;$ we have $\alpha a+\beta b+\gamma c\le |\alpha a+\beta b+\gamma c|\le |\alpha a|+|\beta b|+|\gamma c|.\;$ So
$\displaystyle \alpha a+\beta b+\gamma c\le |a|+|b|+|c|\le 3\sqrt{\frac{|a|^2+|b|^2+|c|^2}{3}}=\sqrt{3}\lt 2.$
Now, with $\alpha=1,\;$ $\beta=1,\;$ $\gamma=a,\;$ this becomes $a+ac+b\le\sqrt{3}\lt 2.$
Illustration
Nassim Nicholas Taleb has kindly produced the following graphics:
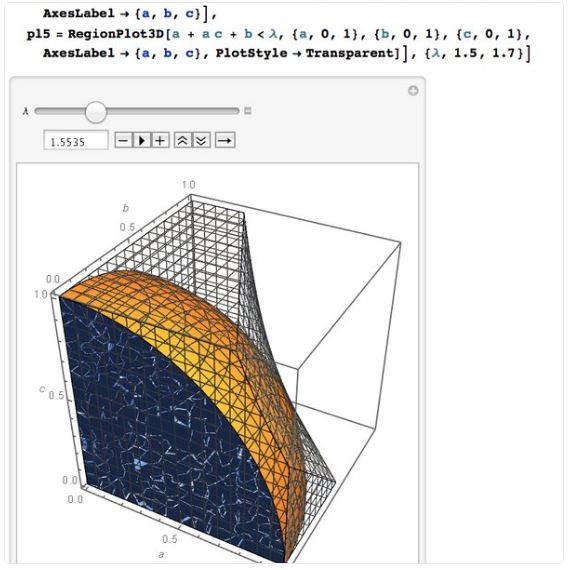
What graphics tells us is that $1.5535\;$ is closer to the smallest bound for $a+ac+b\;$ than $\sqrt{3}.$
Using Lagrange's mulitplier to find $\max (a+ac+b)\;$ subject to $a^2+b^2+c^2=1\;$ produced an approximation, $1.57681.\;$
Improvement
Pradyumna Agashe found this estimate: $\displaystyle a+ac+b\le\frac{19}{12}=1.58\overline{3}.\;$ The proof stems from an equivalent inequality
$\displaystyle \left(\frac{a}{2}-c\right)^2+\left( b-\frac{1}{2}\right)^2+\left(\frac{a\sqrt{3}}{2}-\frac{1}{\sqrt{3}}\right)^2\ge 0.$
Exact solution
Grégoire Nicollier applied Lagrange's multiplier to obtain the exact solution upper bound:
$\displaystyle\sqrt{\frac{47 + (95471 - 5136\sqrt{321})^{1/3} + (95471 + 5136\sqrt{321})^{1/3}}{48}},$
which is $1.5768369\ldots$ Thus the problem should read
For real $a,b,c\;$ that satisfy $a^2+b^2+c^2=1\;$ the following inequality holds:
$\displaystyle a+ac+b\le \sqrt{\frac{47 + \sqrt[3]{95471 - 5136\sqrt{321}} + \sqrt[3]{95471 + 5136\sqrt{321}}}{48}}.$
The maximum is attained once at the point $(a,b,c)\;$ of the unit sphere with $b\gt 0,\;$ $\displaystyle a=\frac{b}{1-b^2},\;$ $\displaystyle c=\frac{b^2}{1-b^2}.\;$ Thus,
$\displaystyle b=\sqrt{\frac{\displaystyle 2 - 8 \sqrt[3]{\frac{2}{3\sqrt{321} -29}} + \sqrt[3]{\frac{3\sqrt{321} -29}{2}}}{3}},\;$
that is, $b\approx 0.53364\ldots$
Related material
| |
Linear Algebra Tools for Proving Inequalities$\;\left(\displaystyle\left(\frac{a}{b-c}\right)^2+\left(\frac{b}{c-a}\right)^2+\left(\frac{c}{a-b}\right)^2\ge 2\right)$ | |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73518392
