A Cyclic Inequality in Three Variables XVIII
Problem
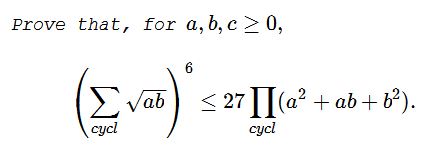
Solution 1
First note that
- $a^2+ab+b^2\ge\displaystyle \frac{3}{4}(a+b)^2\ge 0\,\Longleftrightarrow\,(a-b)^2\ge 0,$
- $a,b,c\gt 0\,\Longrightarrow\,\displaystyle \frac{9}{8}\prod_{cycl}(a+b)\ge\left(\sum_{cycl}a\right)\left(\sum_{cycl}ab\right),$
- $a,b,c\in\mathbb{R}\,\Longrightarrow\,(a+b+c)^2\ge 3(ab+bc+ca).$
It follows that
$\displaystyle \begin{align} \prod_{cycl}(a^2+ab+b^2) &\ge 27\left(\frac{3}{4}\right)^3\prod_{cycl}(a+b)^2\\ &\ge 9(a+b+c)^2(ab+bc+ca)^2. \end{align}$
However,
$9(a+b+c)^2(ab+bc+ca)^2\ge 27(ab+bc+ca)^3.$
Thus, suffice it to prove that
$27(ab+bc+ca)^3\ge (\sqrt{ab}+\sqrt{bc}+\sqrt{ca})^6.$
But, by the Cauchy-Schwarz inequality,
$\displaystyle \begin{align} 27(ab+bc+ca)^3 &\ge 27\left(\frac{(\sqrt{ab}+\sqrt{bc}+\sqrt{ca})^2}{3}\right)^3\\ &\ge (\sqrt{ab}+\sqrt{bc}+\sqrt{ca})^6. \end{align}$
Solution 2
We know that $a^2+ab+b^2\ge\displaystyle \frac{3}{4}(a+b)^2+\frac{(a-b)^2}{4}\ge\frac{3}{4}(a+b)^2.\,$ Similarly, $\displaystyle b^2+bc+c^2\ge\frac{3}{4}(b+c)^2\,$ and $\displaystyle c^2+ca+a^2\ge\frac{3}{4}(c+a)^2,\,$ implying
$\displaystyle\begin{align} 27\prod_{cycl}(a^2+ab+b^2)&\ge 27\cdot\left(\frac{3}{4}\right)^3\prod_{cycl}(a+b)^2\\ &\ge 27\cdot\left(\frac{3}{4}\right)^3\frac{64}{81}\left(\sum_{cycl}a\right)^2\left(\sum_{cycl}ab\right)^2\\ &\ge 27\left(\prod_{cycl}ab\right)^3\\ &\ge \left(\sum_{cycl}\sqrt{ab}\right)^6, \end{align}$
where we used the following inequalities:
- $\displaystyle 9\prod_{cycl}(a+b)\ge 8\left(\sum_{cycl}a\right)\left(\sum_{cycl}ab\right),$
- $(a+b+c)^2\ge 3(ab+bc+ca),$
- $\displaystyle \frac{ab+bc+ca}{3}\ge\left(\frac{\sqrt{ab}+\sqrt{bc}+\sqrt{ca}}{3}\right)^2.$
Solution 3
Lemma 1
For $x,y,z\ge 0,$
(1)
$\displaystyle \left(\sum_{cycl}xy\right)^3\leq \prod(x^2+xy+y^2)$
Indeed, from Hölder's inequality:
$\displaystyle \begin{align} \prod_{cycl}(x^2+xy+y^2)&=(xy+y^2+x^2)(y^2+yz+z^2)(x^2+z^2+xz)\\ &\geq (\sqrt[3]{xy\cdot y^2\cdot x^2}+\sqrt[3]{y^2\cdot yz\cdot z^2}+\sqrt[3]{x^2\cdot z^2\cdot xz})^3\\ &=(xy+yz+zx)^3. \end{align}$
Lemma 2
For $x,y\ge 0,$
(2)
$\displaystyle \left(\sum_{cycl}xy\right)^3\leq 27 \prod_{cycl}(x^2-xy+y^2).$
Indeed,
$(x-y)^2\geq 0\Rightarrow 2(x-y)^2\geq 0\Rightarrow 2x^2-4xy+2y^2\geq 0$
and, finally,
$3x^2-3xy+3y^2\geq x^2+xy+y^2.$
or,
$x^2-xy+y^2\geq \frac{1}{3}(x^2+xy+y^2)\,$
Similarly,
$y^2-yz+z^2\geq \frac{1}{3}(y^2+yz+z^2)\,$ and
$z^2-zx+x^2\geq \frac{1}{3}(z^2+zx+x^2).$
By multiplying the last three relationships,
(3)
$\displaystyle \prod_{cycl}(x^2+xy+y^2)\leq 27 \prod_{cycl}(x^2-xy+y^2).$
Multiplying that by (1) and (2),
$\displaystyle\begin{align} \left(\sum_{cycl}xy\right)^6&\leq 27\prod_{cycl}(x^2+xy+y^2)\cdot \prod_{cycl}(x^2-xy+y^2)\\ &=27\prod_{cycl}\left((x^2+y^2)^2-x^2y^2\right)\\ &=27\prod_{cycl}(x^4+y^4+x^2y^2). \end{align}$
Thus,
(4)
$\displaystyle \left(\sum_{cycl}xy\right)^6=27\prod_{cycl}(x^4+y^4+x^2y^2).$
Setting now in (4) $x=\sqrt{a};\, y=\sqrt{b};\, z=\sqrt{c},\,$ we get
$\displaystyle \left(\sum_{cycl}\sqrt{ab}\right)^6 \le 27\prod_{cycl}(a^2+ab+b^2).$
The equality holds if $a=b=c$.
Solution 4
Case 1: Exactly one of $a,b,c=0$
With $a=0,\,$ the given inequality reduces to $27b^2c^2(b^2+bc+c^2)\ge b^3c^3,\,$ which is obvious. Cases $b=0\,$ and $c=0\,$ are handled similarly.
Case 2: At least two of $a,b,c=0$
The inequality reduces to $0\ge 0.$
Case 3: $a,b,c \gt 0$
Using Wu's inequality, $RHS\ge 27(ab+bc+ca)^3.\,$ Thus, suffice it to prove that
$\begin{align} &27(ab+bc+ca)^3\ge (\sqrt{ab}+\sqrt{bc}+\sqrt{ca})^6,\,\Longleftrightarrow\\ &3(ab+bc+ca)\ge (\sqrt{ab}+\sqrt{bc}+\sqrt{ca})^2,\,\Longleftrightarrow\\ &3\sum_{cycl}x^2\ge\left(\sum_{cycl}x)\right)^2, \end{align}$
where $x=\sqrt{ab},\,$ $y=\sqrt{bc},\,$ $z=\sqrt{ca}.\,$ The latter is true by Hölder's inequality.
Solution 5
We have, by the Power-Mean Inequality, $\displaystyle \left(\frac{1}{3}(\sum_{cycl}(ab)^{\frac{1}{2}}\right)^2\le\frac{1}{3}\sum_{cycl}ab.\,$ Hence
$\displaystyle LHS=\left(\sum_{cycl}(ab)^{\frac{1}{2}}\right)^6\le 3^3\left(\sum_{cycl}ab\right)^3$
and we need to prove that $\displaystyle 3^3\left(\sum_{cycl}ab\right)^3\le RHS,\,$ or
$\displaystyle \left(\sum_{cycl}a^4b^2+\sum_{cycl}a^2b^4+\sum_{cycl}a^4bc\right)-\left(\sum_{cycl}ab^2c^3+\sum_{cycl}a^2b^2c+\sum_{cycl}a^2b^2c^2\right)\ge 0,$
which is true by rearrangement.
Acknowledgment
This problem has been kindly posted at the CutTheKnotMath facebook page by Dan Sitaru and then again by Kevin Soto Palacios, along with his solution (Solution 1). Solution 2 is by Diego Alvariz; Solution 3 is by Dan Sitaru; Solution 4 is by Soumava Chakraborty; Solution 5 is by Nassim Nicholas Taleb. The problem is by Dan Sitaru and has been previously published at the Romanian Mathematical Magazine.
![]()
|Contact| |Up| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73559199
