A Cyclic Inequality in Three Variables XII
Problem
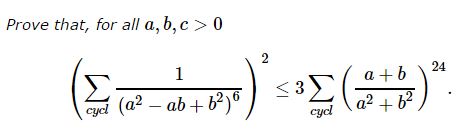
Solution
By Cauchy-Schwarz inequality, $(a^2+b^2)^2\le (a+b)(a^3+b^3),\,$ so that $\displaystyle\frac{1}{a^2-ab+b^2}\le\left(\frac{a+b}{a^2+b^2}\right)^2.\,$ From here, $\displaystyle\frac{1}{(a^2-ab+b^2)^6}\le\left(\frac{a+b}{a^2+b^2}\right)^{12}.\,$ Summing up and, subsequently, applying the AM-QM inequality,
$\displaystyle\begin{align} \left(\sum_{cycl}\frac{1}{(a^2-ab+b^2)^6}\right)^2&\le\left(\frac{a+b}{a^2+b^2}\right)^{12}\\ &\le 3\sum_{cycl}\left(\frac{a+b}{a^2+b^2}\right)^{24}. \end{align}$
Acknowledgment
Dan Sitaru has kindly posted the above problem (from his book "Math Accent") at the CutTheKnotMath facebook page. The solution is by Leo Giugiuc.
![]()
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73607740
