Problem 3980 from Crux Mathematicorum
Problem
Below is Leo Giugiuc's solution to problem 3980 from Crux Mathematicorum. The problem is by S. Viswanathan.
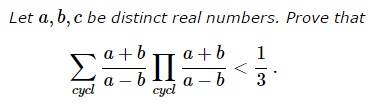
Proof
With $\displaystyle x=\frac{a+b}{a-b},\; y=\frac{b+c}{b-c},\; z=\frac{c+a}{c-a},\;$ we get
$\displaystyle\begin{cases} (1-x)a+(1+x)b=0\\ (1-y)b+(1+y)c=0\\ (1-z)c+(1+z)a=0 \end{cases}$
which can be written in matrix form
$\left(\begin{array}{ccc} \;1-x & 1+x & 0\\ 0 & 1-y & 1+y\\ 1+z & 0 & 1-z \end{array} \right)\left(\begin{array}\;a\\b\\c\end{array}\right)=\left(\begin{array}\;0\\0\\0\end{array}\right).$
Consider the determinant $D=\left|\begin{array}{ccc}\;1-x & 1+x & 0\\0 & 1-y & 1+y\\1+z & 0 & 1-z\end{array}\right|.\;$ If $D\ne 0,\;$ the system admits only a trivial solution: $a=b=c=0\;$ which is inconsistent with the premises of the problem. Thus, $D=0.\;$ But $D=xy+yz+zx+1,\;$ implying
$xy+yz+zx=-1.$
On the other hand, this is a consequence of the Rearrangement Inequality that, for real numbers $u,v,w,\;$ $\displaystyle uv+vw+wu\le\frac{(u+v+w)^2}{3},\;$ with equality only when $u=v=w.$
Hence, $\displaystyle (x+y+z)xyz\le\frac{(xy+yz+zx)^2}{3}=\frac{1}{3}.\;$ Remains it to prove that the inequality is strict. (Leo Giugiuc credits Professor Radu Gologan with this observation.) By the above remark, equality could only hold if $xy=yz=zx.\;$ Since at least one of $xy,yz,zx\;$ is negative, if there is equality then all three are negative: $xy=yz=zx\lt 0.\;$ But this is impossible because $xy\cdot yz\cdot zx=(xyz)^2\ge 0.\;$ It follows that indeed
$\displaystyle\sum_{cycl}\frac{a+b}{a-b}\prod_{cycl}\frac{a+b}{a-b}\lt\frac{1}{3}.$
Related material
| |
Linear Algebra Tools for Proving Inequalities$\;\left(\displaystyle\left(\frac{a}{b-c}\right)^2+\left(\frac{b}{c-a}\right)^2+\left(\frac{c}{a-b}\right)^2\ge 2\right)$ | |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73578894
