A Cyclic Inequality with Many Sums
Problem
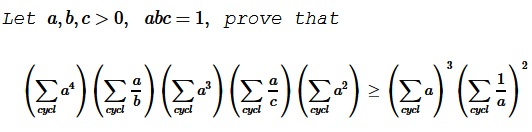
Solution 1
If $n\in \mathbb{N},$
$\displaystyle\begin{align} a^{n+1}+b^{n+1}+c^{n+1} & =a^n\cdot a+b^n\cdot b+c^n\cdot c\\ &\overbrace{\geq}^{Chebyshev}\frac{1}{3}(a^n+b^n+c^n)(a+b+c)\\ &\overbrace{\geq}^{AM-GM} \frac{1}{3}(a^n+b^n+c^n)\cdot 3\sqrt[3]{abc}\\& =\frac{1}{3}(a^n+b^n+c^n)\cdot 3\\ &=a^n+b^n+c^n. \end{align}$
It follows that
$a^4+b^4+c^4\geq a^3+b^3+c^3\geq a^2+b^2+c^2\geq a+b+c.$
In particular, $\displaystyle\sum_{cycl}a^4\ge\sum_{cycl}a\,(1)\,$ and $\displaystyle\sum_{cycl}a^2\ge\sum_{cycl}a.\,(2).$
Further,
$\displaystyle\begin{align} \sum_{cycl}a^3 &=a^3+b^3+c^3=a^2\cdot a+b^2\cdot a+c^2\cdot c\\ &\overbrace{\geq}^{Chebyshev} \frac{1}{3}(a^2+b^2+c^2)(a+b+c)\\ &\overbrace{\geq}^{AM-GM} \frac{1}{3}(a^2+b^2+c^2)\cdot 3\sqrt[3]{abc}\\ &=\frac{1}{3}(a^2+b^2+c^2)\cdot 3=a^2+b^2+c^2\\ &\geq ab+bc+ca=\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\sum_{cycl}\frac{1}{a}, \end{align}$
So that $\displaystyle\sum_{cycl}a^3\geq \sum_{cycl}\frac{1}{a}\,(3).$ By the AM-GM inequality,
$(4)\qquad\displaystyle a=\sqrt[3]{\frac{a}{b}\cdot \frac{a}{b}\cdot \frac{b}{c}}\leq \frac{\frac{a}{b}+\frac{a}{b}+\frac{b}{c}}{3}\\ (5)\qquad\displaystyle b=\sqrt[3]{\frac{b}{c}\cdot \frac{b}{c}\cdot \frac{c}{a}}\leq \frac{\frac{b}{c}+\frac{b}{c}+\frac{c}{a}}{3}\\ (6)\qquad\displaystyle c=\sqrt[3]{\frac{c}{a}\cdot \frac{c}{a}\cdot \frac{a}{b}}\leq \frac{\frac{c}{a}+\frac{c}{a}+\frac{a}{b}}{3}$
By adding (4),(5),(6), $\displaystyle\sum^{cycl}\frac{a}{b}\ge\sum_{cycl}a\;(7)\,$ and, by analogy with (4)-(6),
$(8)\qquad\displaystyle\frac{1}{a}=\sqrt[3]{\frac{b}{a}\cdot \frac{b}{a}\cdot \frac{a}{c}}\leq \frac{\frac{b}{a}+\frac{b}{a}+\frac{a}{c}}{3}\\ (9)\qquad\displaystyle\frac{1}{b}=\sqrt[3]{\frac{c}{b}\cdot\frac{c}{b}\cdot \frac{b}{a}}\leq \frac{\frac{c}{b}+\frac{c}{b}+\frac{c}{b}}{3}\\ (10)\qquad\displaystyle\frac{1}{c}=\sqrt[3]{\frac{a}{c}\cdot \frac{a}{c}\cdot \frac{c}{b}}\leq \frac{\frac{a}{c}+\frac{a}{c}+\frac{c}{b}}{3}$
By adding the relationships (8),(9),(10), $\displaystyle\sum_{cycl}\frac{a}{c}\ge\sum_{cycl}\frac{1}{a}\,(11).$
The product of (1), (2), (3), (7), (11) is exactly
$\displaystyle \left(\sum_{cycl}a^4\right)\left(\sum_{cycl}\frac{a}{b}\right)\left(\sum_{cycl}a^3\right)\left(\sum_{cycl}\frac{a}{c}\right)\left(\sum_{cycl}a^2\right) \ge \left(\sum_{cycl}a\right)^3\left(\sum_{cycl}\frac{1}{a}\right)^2.$
Solution 2
By the AM-GM inequality, $\displaystyle\sum_{cycl}a\ge 3,\,$ so that $\displaystyle\left(\sum_{cycl}a\right)^3\ge 9\left(\sum_{cycl}a\right).\,$ But $\displaystyle 9\left(\sum_{cycl}a^3\right)\ge\left(\sum_{cycl}a\right)^3.\,$ Combining all these gives $\displaystyle\sum_{cycl}a^3\ge\sum_{cycl}a.$
By Hölder's inequality, $\displaystyle\left(\sum_{cycl}a^4\right)\left(\sum_{cycl}a^3\right)\left(\sum_{cycl}a^2\right)\ge\left(\sum_{cycl}a^3\right)^3,\,$ implying $\displaystyle\left(\sum_{cycl}a^4\right)\left(\sum_{cycl}a^3\right)\left(\sum_{cycl}a^2\right)\ge\left(\sum_{cycl}a\right)^3.\,$ On the other hand, $\displaystyle\left(\sum_{cycl}\frac{1}{a}\right)^2=\left(\sum_{cycl}ab\right)^2.\,$
As in (11) of Solution 1, $\displaystyle\sum_{cycl}\frac{a}{b}\ge\sum_{cycl}\frac{1}{a}\,$ so that $\displaystyle\left(\sum_{cycl}\frac{a}{b}\right)\left(\sum_{cycl}\frac{a}{c}\right)\ge\left(\sum_{cycl}\frac{1}{a}\right)^2\,$ which completes the proof.
Solution 3
We proceed in several steps:
Due to the condition $abc=1,\,$ the AM-GM inequality implies that, $\displaystyle\sum_{cycl}a^p\ge 3,\,$ for any real $p.$
$\displaystyle\sum_{cycl}a^3\ge\sum_{cycl}a.\,$ More generally, $\displaystyle\sum_{cycl}a^{p+q}\ge\sum_{cycl}a^{p}.$ Indeed, by the hierarchy of the means, $\displaystyle\left(\frac{1}{3}\sum_{cycl}a^{p+q}\right)^{\frac{1}{p+q}}\ge\left(\frac{1}{3}\sum_{cycl}a^p\right)^{\frac{1}{p}},\,$ i.e., $\displaystyle \frac{1}{3}\sum_{cycl}a^{p+q}\ge\left(\frac{1}{3}\sum_{cycl}a^p\right)^{\frac{p+q}{p}},\,$ or,
$\displaystyle\begin{align} \sum_{cycl}a^{p+q} &\ge\frac{3}{3^{\frac{p+q}{p}}}\left(\sum_{cycl}a^p\right)^{\frac{p+q}{p}}\ge\frac{3}{3^{\frac{p+q}{p}}}\left(\sum_{cycl}a^p\right)^{\frac{3}{3}}\cdot 3^{\frac{q}{p}}\\ &=\sum_{cycl}a^p. \end{align}$
$\displaystyle\left(\sum_{cycl}a^4\right)\left(\sum_{cycl}a^3\right)\left(\sum_{cycl}a^2\right)\ge\left(\sum_{cycl}a^3\right)^3.$
This is a direct application of Hölder's inequality.
$\displaystyle\left(\sum_{cycl}\frac{a}{b}\right)\left(\sum_{cycl}\frac{a}{c}\right)\ge\left(\sum_{cycl}\frac{1}{a}\right)^2.$
We replace this with
$\displaystyle(a^2b+b^2c+c^2a)(ab^2+bc^2+ca^2)\ge (ab+bc+ca)^2.$
This is true because $(ab)(bc)(ca)=1\,$ and, applying #2 to these three numbers and using Hölder's inequality,
$\displaystyle(a^2b+b^2c+c^2a)(ab^2+bc^2+ca^2)\ge ((ab)^{\frac{3}{2}}+(bc)^{\frac{3}{2}}+(ca)^{\frac{3}{2}})^2\ge (ab+bc+ca)^2.$
Acknowledgment
Dan Sitaru has kindly posted the problem from his book Math Accent at the CutTheKnotMath facebook page and supplied his solution (Solution 1) on a tex file. Solution 2 is by Leo Giugiuc; Solution 3 is by N. N. Taleb
![]()
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73582682
