A Cyclic Inequality in Three Variables XIV
Problem
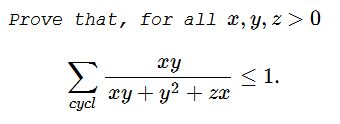
Solution
With the Cauchy-Schwarz inequality, we get
$\displaystyle\begin{align} \sum_{cycl}\frac{xy}{xy+y^2+zx} &= \sum_{cycl}\frac{\displaystyle xy\left(\frac{x}{y}+1+\frac{z}{x}\right)}{\displaystyle (xy+y^2+zx)\left(\frac{x}{y}+1+\frac{z}{x}\right)}\\ &\le\sum_{cycl}\frac{x^2+xy+yz}{(x+y+z)^2}\\ &=\frac{(x+y+z)^2}{(x+y+z)^2}\\ &=1. \end{align}$
Acknowledgment
This problem has been shared by Mihai Dicu at the Olimpiada pe Scoala (The School Yard Olympiad) facebook group. The beautiful solution is by Diego Alvariz.
![]()
|Contact| |Up| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73549680
