$ab + bc + ca \le aa + bb + cc$

What Is That About?

Created with GeoGebra

Problem

The inequality below, though simple, is useful and often comes up in proofs of more involved inequalities. Here, I'd like to document several of its proofs.

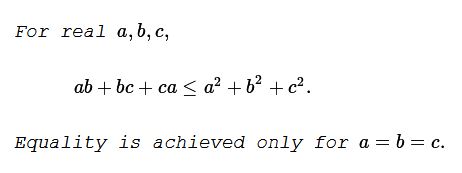
ab + bc + ca does not exceed aa + bb + cc

Proof 0

This proof is illustrated by the applet above. It was suggested by Teo López Puccio.

The bottom segment is split into three of lengths $a,\,$ $b,\,$ and $c.\,$ We assume $a\ge b\ge c.\,$ For the value of the slider $u=1,\,$ the total colored area equals $ab+bc+ca.\,$ When the value of the slider $u=0,\;$ the total colored area equals $a^2+b^2+c^2.\,$ One can observe that the former could not exceed the latter.

Proof 1

By the AM-GM inequality, $\displaystyle xy\le\frac{x^2+y^2}{2}.\;$ So we have

$\displaystyle\begin{align} ab+bc+ca &\le \left(\frac{a^2+b^2}{2}\right)+\left(\frac{b^2+c^2}{2}\right)+\left(\frac{c^2+a^2}{2}\right)\\ &=a^2+b^2+c^2. \end{align}$

Proof 2

WLOG, we may assume, say, $a\le b\le c.\;$ Then by the Rearrangement Inequality,

$ab + bc + ca \le aa + bb + cc=a^2 + b^2 + c^2.$

Proof 3

Observe the obvious $(a-b)^2+(b-c)^2+(c-a)^2\ge 0.\;$ This is equivalent to

$2(a^2+b^2+c^2)\ge 2(ab + bc + ca).$

Proof 4

$\displaystyle\sum_{cycl}a^2-\sum_{cycl}ab=\frac{1}{2}\sum_{cycl}(a-b)^2\ge 0.$

Proof 5

The function $\displaystyle f(a,b,c)=\sum_{cycl}a^2-\sum_{cycl}ab\;$ is homogeneous of degree $2:\;$ $f(ta,tb,tc)=t^2f(a,b,c),\;$ for $t\ne 0.\;$ Thus, we may apply various normalizations, e.g., $a=1,\;$ $b=1+x,\;$ $c=1+y.\;$ The substitution transforms the inequality into

$(1+x)+(1+x)(1+y)+(1+y)\le 1+(1+x)^2+(1+y)^2,$

which reduces to

$(1+x)+(1+x)(1+y)+(1+y)\le 1+(1+x)^2+(1+y)^2,$

and, subsequently, to $xy\le x^2+y^2.$ But from $(x-y)^2\ge 0\;$ it follows that already $\displaystyle xy\le\frac{1}{2}(x^2+y^2)\;$ which is stronger than $xy\le x^2+y^2.$

Proof 6

Reaching $xy\le x^2+y^2$ as in the previous proof, we observe that this is equivalent to $\displaystyle 0\le\left(x-\frac{y}{2}\right)^2+\frac{3y^2}{4}.$

Proof 7

Let's denote $p=a+b+c\;$ and $q=ab+bc+ca.\;$ $a,b,c\;$ are the roots of a third-degree polynomial $f(t)=t^3-pt^2+qt-abc.\;$ Since this polynomial has three real roots $a,b,c,\;$ its derivative $f'(t)=3t^2-2pt+q\;$ has two real roots, meaning that its discriminant is not negative: $p^2-3q\ge 0.$ In terms of $a,b,c\;$ this is exactly the required inequality.

Proof 8

Let's consider a second degree polynomial $f(x)=x^2-x(b+c)+(b^2+c^2-bc).\;$ The discriminant of this polynomial,

$D=(b+c)^2-4(b^2+c^2-bc)=-3(b-c)^2\lt 0,$

meaning that $f(t)\;$ has no real roots (unless $b=c)\;$ and, consequently, is of the same sign for all $t\in\mathbb{R}.\;$ Since it is obviously positive for large values of $t,\;$ it is positive everywhere. In particular, if $b\ne c,\;$ $f(a)\gt 0.\;$ From the quadratic formula $f(a)=0,\;$ iff $a=b=c.$

Proof 9

This proof has been communicated by Leo Giugiuc.

By the Ionescu-Weitzenbock inequality, $x^2+y^2+z^2\ge 4\sqrt{3}S,\;$ where $S=[\Delta ABC],\;$ the area of an acute triangle $ABC\;$ and $x,y,z\;$ its side lengths.

Let $x^2=b^2+c^2,\;$ $y^2=c^2+a^2,\;$ $z^2=a^2+b^2,\;$ where $a,b,c\;$ are real numbers. $2S=\sqrt{a^2b^2+b^2c^2+c^2a^2}.\;$ So we have

$a^2+b^2+c^2\ge \sqrt{3(a^2b^2+b^2c^2+c^2a^2)}.\;$

But

$\begin{align} \sqrt{3(a^2b^2+b^2c^2+c^2a^2)}&\ge|ab|+|bc|+|ca|\\ &\ge ab+bc+ca.\;\end{align}$

Proof 10

This illustration is by Nassim Nicholas Taleb.

geometric illustration for ab+bc+ca does not exceed aa+bb+cc, #1

Graphical representation: ridge a=b for different values of c. Can't get a clean RegionPlot3D.

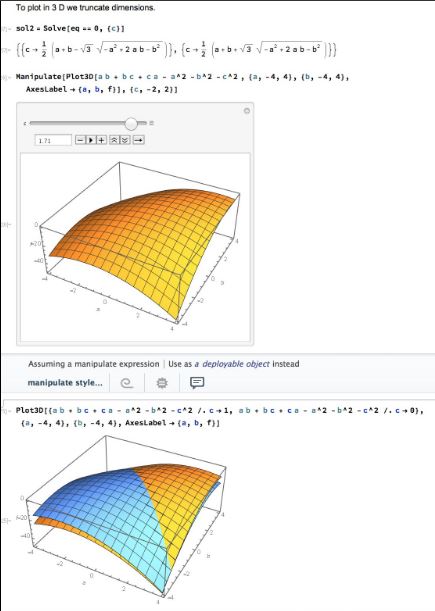
geometric illustration for ab+bc+ca does not exceed aa+bb+cc, #2

Finally, as we converge to equality from below.

geometric illustration for ab+bc+ca does not exceed aa+bb+cc

Proof 11

Kunihiko Chikaya posted the following proof with the comment: "Here is the solution to Japanese Kids at age of 13, 14, 15."

$\begin{align} f(a) &= a^2 + b^2 + c^2 - ab - bc - ca\\ &= a^2 - (b + c ) a + b^2 - bc + c^2\\ &= [a - (b + c) / 2] ^2 + (3/4)\cdot (b-c)^2\\ &\ge 0. \end{align}$

Equality holds if only if $a - (b + c) / 2 = 0\;$ and $b - c = 0,\;$ $a = b = c.$

Proof 12

Sam Walters has observed that the inequality is a one step application of the Cauchy-Schwarz inequality:

$ab+bc+ca \le \sqrt{a^2+b^2+c^2}\cdot\sqrt{b^2+c^2+a^2}=a^2+b^2+c^2.$

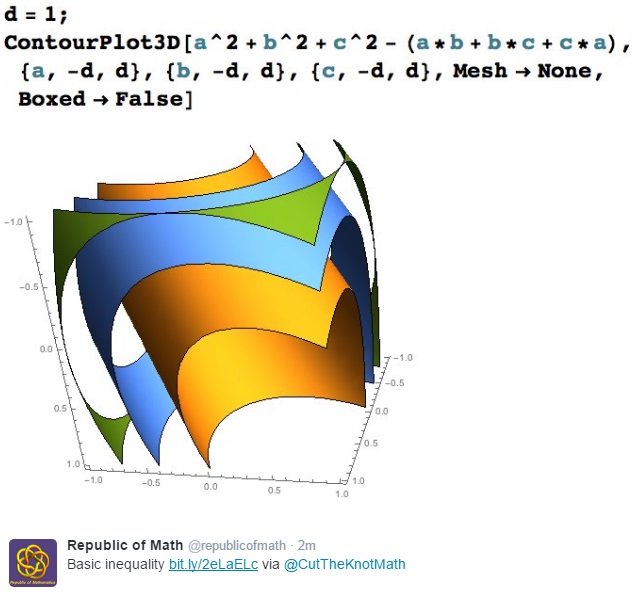
Illustration

Here's an illustration by Gary Davis.

Basic inequality, illustration

References

  1. A. Engel, Problem-Solving Strategies, Springer Verlag, 1998

 

Cyclic inequalities in three variables

|Contact| |Front page| |Contents| |Algebra|

Copyright © 1996-2018 Alexander Bogomolny

72392339