A Cyclic Inequality in Three Variables XVII
Problem
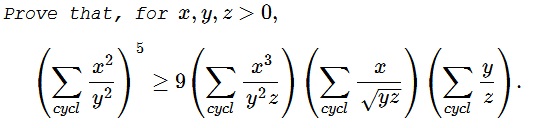
Solution 1
Let $\displaystyle \frac{x}{y}=a^2,\,$ $\displaystyle \frac{y}{z}=b^2,\,$ $\displaystyle \frac{z}{x}=c^2.\,$ Then $abc=1\,$ and the required inequality becomes
$\displaystyle \left(\sum_{cycl}a^4\right)^5\ge 9\left(\sum_{cycl}\frac{a^4}{c^2}\right)\left(\sum_{cycl}\frac{a}{c}\right)\left(\sum_{cycl}a^2b^2\right).$
But, since $a+b+c\ge 3,\,$ Hölder's inequality gives $\displaystyle \sum_{cycl}a^4\ge\sum_{cycl}a^3.\,$ Also, $\displaystyle \sum_{cycl}\frac{a}{c}=\sum_{cycl}a^2b\,$ and $\displaystyle \sum_{cycl}a^3\ge\sum_{cycl}a^2b,\,$ so that $\displaystyle \sum_{cycl}a^4\ge\sum_{cycl}\frac{a}{c}.$
By the Rearrangement inequality, $\displaystyle \sum_{cycl}a^4\ge\sum_{cycl}a^2b^2.$
On the other hand, $\displaystyle\sum_{cycl}\frac{a^4}{c^2}=\sum_{cycl}a^6b^2\,$ and, according to an inequality by Vasile Cirtoaje, $\displaystyle\left(\sum_{cycl}a^4\right)^2\ge 3\sum_{cycl}a^6b^2.\,$ Finally, $\displaystyle \sum_{cycl}a^4\ge 3,\,$ by the AM-GM inequality.
The required inequality results as the product of
$\begin{align} \sum_{cycl}a^4&\ge\sum_{cycl}\frac{a}{c},\\ \sum_{cycl}a^4&\ge\sum_{cycl}a^2b^2,\\ \left(\sum_{cycl}a^4\right)^2&\ge \left[3\sum_{cycl}a^6b^2=\right]\,3\sum_{cycl}\frac{a^4}{c^2},\\ \sum_{cycl}a^4&\ge 3. \end{align}$
Solution 2

Acknowledgment
This problem has been kindly posted at the CutTheKnotMath facebook page by Leo Giugiuc, along with his solution. The problem by Dan Sitaru has been previously posted at the Romanian Mathematical Magazine. Solution 2 is by N. N. Taleb.
![]()
|Contact| |Up| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73573519
