An Inequality from a Vietnamese Problem Book
Problem
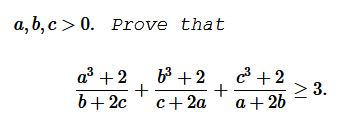
Solution 1
By the AM-GM inequality, $a^3+2\ge 3a,\,$ $b^3+2\ge 3b,\,$ $c^3+2\ge 3c.\,$ Suffice it to show that
$\displaystyle \frac{a}{b+2c}+\frac{b}{c+2a}+\frac{c}{a+2b}\ge 1.$
Let $\displaystyle \frac{a}{b+2c}=x,\,$ $\displaystyle \frac{b}{c+2a}=y,\,$ $\displaystyle \frac{c}{a+2b}=z.\,$ Then $x,y,z\gt 0\,$ and
$\left(\begin{array}{ccc}\,-1&x&2x\\2y&-1&y\\z&2z&-1\end{array}\right)\left(\begin{array}{c}\,a\\b\\c\end{array}\right)=\left(\begin{array}{c}\,0\\0\\0\end{array}\right).$
If the matrix here is invertible, the only solution that the system may have is trivial, but, by the definition, the system has a non-trivial solution $(a\,b\,c)^t,\,$ implying that the determinant of the matrix vanishes:
$\left|\begin{array}{ccc}\,-1&x&2x\\2y&-1&y\\z&2z&-1\end{array}\right|=0.$
It follows that $2(xy+yz+zx)+9xyz=1.\,$ Le $x+y+z=t.\,$ Thne $\displaystyle \frac{2t^2}{3}\ge 2(xy+yz+zx)\,$ and $\displaystyle \frac{t^3}{3}\ge 9xyz,\,$ such that $t^3+2t^2\ge 3,\,$ i.e., $(t-1)(t^2+3t+3)\ge 0,\,$ so that $t\ge 1.\,$ This completes the proof.
Solution 2
Using Bergstrom's inequality,
$\displaystyle \begin{align} \sum_{cycl}\frac{a^3+2}{b+2c}&=\sum_{cycl}\frac{a^4}{ab+2ac}+2\sum_{cycl}\frac{1}{b+2c}\\ &\ge\frac{(a^2+b^2+c^2)^2}{3(ab+bc+ca)}+\frac{2\cdot 3^2}{3(a+b+c)}\\ &\ge\frac{a^2+b^2+c^2}{3}+\frac{6}{a+b+c}\\ &\ge\frac{(a+b+c)^2}{9}+\frac{3}{a+b+c}+\frac{3}{a+b+c}\\ &\ge 3\sqrt[3]{\frac{(a+b+c)^2}{9}\cdot\frac{3}{a+b+c}\cdot\frac{3}{a+b+c}}\\ &=3, \end{align}$because $a^2+b^2+c^2\ge ab+bc+ca\,$ and $3(a^2+b^2+c^2)\ge (a+b+c)^2.$
Solution 3
We start with $\displaystyle \sum_{cycl}\frac{a}{b+2c}.\,$ Using Bergstrom's inequality,
$\displaystyle \sum_{cycl}\frac{a}{b+2c}\ge\frac{\displaystyle \left(\sum_{cycl}a\right)^2}{\displaystyle \sum_{cycl}(ab+2ac)}=\frac{\displaystyle \left(\sum_{cycl}a\right)^2}{\displaystyle 3\sum_{cycl}ab}\ge\frac{\displaystyle \left(\sum_{cycl}a\right)^2}{\displaystyle 3\frac{1}{3}\left(\sum_{cycl}a\right)^2}=1,$
because $(a+b+c)^2=(a^2+b^2+c^2)+2(ab+2bc+ca)\ge 3(ab+2bc+ca).$
Acknowledgment
Leo Giugiuc has kindly mailed me the problem and his solution (Solution 1) that shows once again how useful linear algebra may be in proving inequalities. The problem was originally posted by Imad Zak at the mathematical inequalities facebook group. Solution 2 is by Abdur Rehman Zahid.
Related material
| |
Linear Algebra Tools for Proving Inequalities$\;\left(\displaystyle\left(\frac{a}{b-c}\right)^2+\left(\frac{b}{c-a}\right)^2+\left(\frac{c}{a-b}\right)^2\ge 2\right)$ | |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
![]()
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73585285
