An Inequality from Gazeta Matematica, March 2016
Problem
An inequality with two solutions by Dan Sitaru and Leo Giugiuc has been just published in Gazeta Matematica (March 2016).
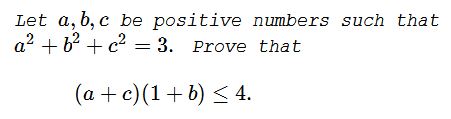
Proof 1
Define matrix $\displaystyle A=\left(\begin{array}\;1&a\\a&b\\b&c\\c&1\end{array}\right).\;$ We have
$\displaystyle\begin{align} A^t\cdot A &= \left(\begin{array}\;1&a&b&c\\a&b&c&1\end{array}\right)\cdot \left(\begin{array}\;1&a\\a&b\\b&c\\c&1\end{array}\right)\\ &=\left(\begin{array}\;a^2+b^2+c^2+1 & a+ab+bc+c\\a+ab+bc+c & a^2+b^2+c^2+1\end{array}\right)\\ &=\left(\begin{array}{c,c}\;4 & (a+c)(1+b)\\(a+c)(1+b) & 4\end{array}\right). \end{align}$
By Cauchy-Binet theorem, $\text{det}(A^t\cdot A)\ge 0.\;$ Therefore, $[(a+c)(1+b)]^2\le 16,\;$ or, $(a+c)(1+b)\le 4.$
Proof 2
We use spherical coordinates. Let $b=\sqrt{3}\cos t,\;$ $a=\sqrt{3}\sin t \cos u,\;$ and $c=\sqrt{3}\sin t \sin u,\;$ where $\displaystyle 0\lt t\lt\frac{\pi}{2}.\;$ We need to prove that $\sqrt{3}(\cos u+\sin u)(1+\sqrt{3}\cos t)\sin t\le 4.$
Observe that $1\lt \sin u+\cos u\le\sqrt{2}.\;$ Thus, suffice it to prove that $\sqrt{6}(1+\sqrt{3}\cos t)\sin t\le 4.$
Consider the function $\displaystyle f;\,\left(0,\frac{\pi}{2}\right)\rightarrow\mathbb{R},\;$ defined by $f(t)=(1+\sqrt{3}\cos t)\sin t.\;$ We have $f'(t)=2\sqrt{3}\cos^2t+\cos t-\sqrt{3}\sin t\;$ which implies $\displaystyle \text{max}f=f\left(\arccos\left(\frac{1}{\sqrt{3}}\right)\right)=2\sqrt{\frac{2}{3}}.\;$ Therefore, $\displaystyle \sqrt{6}(1+\sqrt{3}\cos t)\sin t\le\sqrt{6}\cdot 2\sqrt{\frac{2}{3}}=4.$
Proof 3
$(a-b)^2+(b-c)^2+(a-1)^2+(c-1)^2\ge 0\;$ which simplifies to $(a^2+b^2+c^2)+1-ab-bc-a-c\ge 0.\;$ This is exactly $(a+c)(1+b) \le 4.$
Proof 4
By the AM-QM inequalty, $\displaystyle\frac{a+b+c}{3}\le\sqrt{\frac{a^2+b^2+c^2}{3}}=1.\;$ Further, by the AM-GM inequality,
$\displaystyle\begin{align} (a+c)(b+1) &\le \left(\frac{a+c+b+1}{2}\right)^2\\ &\le \left(\frac{3+1}{2}\right)^2\\ &=4. \end{align}$
Proof 5
From $a^2+b^2+c^2=3,\;$ $3\sum a^2\ge\left(\sum a\right)^2,\;$ implying $\left(\sum a\right)^2\le 9,\;$ or, $a+b+c\le 3.\;$ $a+b+c+1\le 4.\;$ Therefore,
$4\ge (a+c)+(b+1)\ge 2\sqrt{(a+c)(b+1)},\;$ i.e., $2\ge \sqrt{(a+c)(b+1)},\;$ or $4\ge (a+c)(b+1).$Equality is attained when $a+c=b+1,\;$ which, with $a^2+b^2+c^2=3\;$ implies $a=b=c=1.$
Proof 6
From $(x-y)^2\ge 0\;$ we have $2xy\le x^2+y^2.\;$ We use this with the couples $(a,b),\;$ $(b,c),\;$ $(1,a),\;$ $(1,c):\;$
$2ab\le a^2+b^2\\ 2bc\le b^2+c^2\\ 2a\le 1+a^2\\ 2c\le 1+c^2$
adding which gives $2(a+c+ab+bc)\le 2+2(a^2+b^2+c^2)=8,\;$ and this is exactly $(a+c)(b+1)\le 4.$
Proof 7
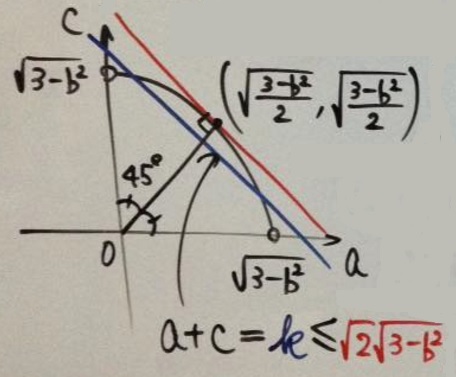
To continue:
$\displaystyle\begin{align} (a+c)(1+b) &\le \sqrt{2}\sqrt{3-b^2}(1+b)\\ &\le\sqrt{2}\sqrt{4-2b})1+b)\\ &=\sqrt{2}\sqrt{(4-2b)(1+b)^2}\\ &=\sqrt{2}\sqrt{(1+b)(1+b)(4-2b)}\\ &\le\sqrt{2}\sqrt{\left(\frac{1+b+1+b+4-2b}{3}\right)^3}\\ &=4. \end{align}$
The equality is achieved for $1+b=1+b=4-2b,\;$ making $b=1\;$ which, by the way, satisfies $3-b^2\ge 0.\;$ $\displaystyle a=c=\sqrt{\frac{3-b^2}{2}},\;$ i.e., $a=b=c=1.$
Proof 8
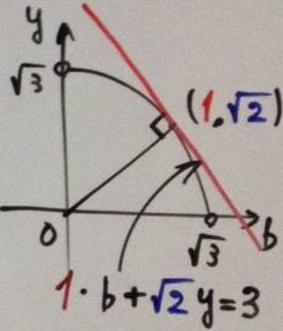
To continue:
$\displaystyle\begin{align} (a+c)(1+b) &\le \sqrt{2}\sqrt{3-b^2}(1+b)\\ &\le\sqrt{2}\frac{3-b}{\sqrt{2}}(1+b)\\ &\le\left(\frac{3-b+1+b}{2}\right)^2\\ &=4. \end{align}$
Equality is achieved for $3-b=1+b\;$ and $\displaystyle a=c=\sqrt{\frac{3-b^2}{2}},\;$ i.e., $a=b=c=1.$
Proof 9
Observe that $(a+c)(1+b)=a\cdot 1+a\cdot b+c\cdot 1+b\cdot c\;$ such that by the Cauchy-Schwarz inequality,
$(a\cdot 1+a\cdot b+c\cdot 1+b\cdot c)^2 \le (a^2+b^2+c^2+b^2)(1^2+a^2+1^2+c^2)$
which leads to a chain of inequalities
$\displaystyle\begin{align} (a+ab+c+bc)^2 &\le (3+b^2)(2+a^2+c^2)\\ \left[(a+c)(1+b)\right]^2 &\le (3+b^2)(2+3-b^2)\\ &= (3+b^2)(5-b^2)\\ &\le \left[\frac{3+b^2+5-b^2}{2}\right]^2\\ &= \left[\frac{8}{2}\right]^2, \end{align}$
and, therefore, $(a+c)(1+b)\le 4.$
Proof 10
From $(a+c)^2\le 2(a^2+c^2)\;$ and $(1+b)^2\le 2(1+b^2)\;$ we obtain a sequence of inequalities:
$\displaystyle\begin{align} (a+c)^2(1+b)^2 &\le 4(a^2+c^2)(1+b^2)\\ &\le 4\left(\frac{a^2+c^2+1+b^2}{2}\right)^2\\ &= 4\left(\frac{4}{2}\right)^2\\ &= 4\cdot 4. \end{align}$
and, therefore, $(a+c)(1+b)\le 4.$
Proof 11
We prove $((a+b)(1+c))^2\le 16\;$ when the point $(a,b,c)\;$ lies on the sphere of radius $\sqrt{3}\;$ centered at the origin. At height $c\;$ the sphere is a circle of radius $r=\sqrt{3-c^2}\;$ and the maximum of $a+b\;$ is $r\sqrt{2}\;$ (consider the line with slope $-1\;$ tangent to this circle in the first quadrant of the plane). We want thus the maximum of $2(1+c)^2 (3-c^2)\;\;$ for $0 \le c \le \sqrt{3}.\;$ The value $16\;$ is attained for $c=1.\;$ But $16 - 2(1+c)^2 (3-c^2) = 2(c-1)^2 (5 + 4 c + c^2)\ge 0,\qquad$ for all real $c.$
Proof 12
Use Lagrange multipliers to prove that
(1)
$\displaystyle\max_{a^2+b^2+c^2=3}(a+c)(1+b)=4.$
Let $J=(a+c)(1+b)+\lambda (a^2+b^2+c^2-3).$
Taking $\displaystyle\frac{\partial J}{\partial a}=\frac{\partial J}{\partial b}=\frac{\partial J}{\partial c}=\frac{\partial J}{\partial\lambda}=0\;$ yields
(2)
$1+b+2a\lambda=0,$
(3)
$1+c+2b\lambda=0,$
(4)
$1+b+2c\lambda=0,$
(5)
$a^2+b^2+c^2=3.$
(6)
$a=c\;$ (from (2) and (4))
(7)
$2a^2+2ab\lambda=0\;$ (from (3) and(6))
(8)
$b+b^2+2ab\lambda=0\;$ (from (2))
(9)
$b+b^2=2a^2\;$ (from (7) and (8))
(10)
$2a^2+b^2=3$ (from (5) and (6))
(11)
$2b^2+b-3=0,\; b=1,-3/2$ (from (9) and (10))
Hence, $b=1\;$ and from (10), $a=\pm 1,\;$ implying $a=c=1\;$ and $b=1,\;$ and (1) follows.
Remark
It is clear that the equality is attained for $a=b=c=1\;$ - a symmetric condition whereas the inequality itself is asymmetric. In analogy with the above derivation, we can show $(b+a)(1+c)\le 4\;$ and $(b+c)(1+a)\le 4.\;$ The sum of the three gives $(a+b+c)+(ab+bc+ca)\le 6\;$ which is just more symmetric.
Acknoledgment
Proofs 1 and 2 are by Leo Giugiuc and Dan Sitaru; Proof 3 is by Nevena Sybeva; Proof 4 is by Augustini Moraru; Proof 5 is by Imad Zak and independently by Rahim Shahbazov; Proof 6 is by Robert Kosova; Proofs 7 and 8 are by Kunihiko Chikaya; Proofs 9 and 10 are by Sk Rejuan; Proof 11 is by Grégoire Nicollier; Proof 12 is by Michalos Nikolau. My sincerest gratitud goes to Leo Giugiuc for furnishing this collection.
Related material
| |
Linear Algebra Tools for Proving Inequalities$\;\left(\displaystyle\left(\frac{a}{b-c}\right)^2+\left(\frac{b}{c-a}\right)^2+\left(\frac{c}{a-b}\right)^2\ge 2\right)$ | |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73582382
