Four Touching Circles IV
I have discussed on several opportunities a configuration of a chain of four pairwise touching circles. The salient feature of the configuration is that the four points of tangency are concyclic, provided that the number of external tangencies between the circles is even. The configuration has number of additional properties.
First of all, if the points of tangencies are concyclic, the center of their circumcircle is - naturally - the radical center of all four given circles, the common point of the four common tangents.
If we combine the circles into non-touching pairs, then the centers of similitude of the circles in one pair lie on the radical axis of the other pair. Shortening the description with mathematical notations permits a stronger, more accurate statement:
Given a chain of circles \(S(AB)\), \(T(BC)\), \(U(CD)\), and \(V(DA),\) with centers at \(S,T,U,V\) and touching pairwise (externally) at the points \(A,B,C,D.\) Points \(A,B,C,D\) are necessarily concyclic, with the circumcircle \(O(ABCD)\) being centered at the common radical center \(O\) of the four given circles. In addition, the external center of similitude of circles \(T(BC)\) and \(V(DA)\) coincides with the radical center of circles \(S(AB)\) and \(U(CD),\) and \(O(ABCD)\).
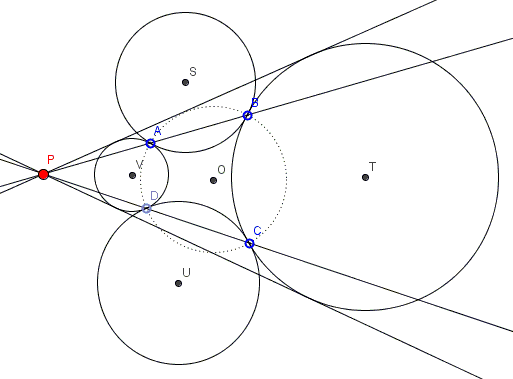
The applet below serves to illustrate the problem:
|Contact| |Front page| |Content| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
Given a chain of circles \(S(AB)\), \(T(BC)\), \(U(CD)\), and \(V(DA),\) with centers at \(S,T,U,V\) and touching pairwise (externally) at the points \(A,B,C,D.\) Points \(A,B,C,D\) are necessarily concyclic, with the circumcircle \(O(ABCD)\) being centered at the common radical center \(O\) of the four given circles. In addition, the external center of similitude of circles \(T(BC)\) and \(V(DA)\) coincides with the radical center of circles \(S(AB)\) and \(U(CD),\) and \(O(ABCD)\).

In the diagram, \(AB\) and \(CD\), being radical axes of \(S(AB)\), \(O(ABCD)\) and, respectively, \(U(CD)\), \(O(ABCD)\) of meet at the radical center \(P\) of the three circles. This, in particular, means that \(P\) has equal power with respect to circles \(S(AB)\) and \(U(CD)\):
\( r^{2}=PA\cdot PB=PC\cdot PD, \)
implying that the inversion with center \(P\) and radius \(r\), inverts \(A\) into \(B\) and \(C\) into \(D\). This, in turn, implies that \(A\) and \(B\) are antihomologous with respect to the associated homothety with center \(P\) that maps \(V(DA)\) to \(T(BC),\) thus serving the center of similitude of the two circles.
The conclusion may be a little weakened: if the four circles are split into two pairs of not touching circles (although they mey cross), then the radical axis of one pair passes through the centers of the similitudes of the other pair.
The applet allows to verify that the claim remains true even when the four tangencies are not all external.
It may be worth observing that, say, line \(AB\) serves as the axis of similitude of the three circles \(S(AB)\), \(V(DA)\), and \(T(BC).\) This is because, \(A\) is a center of similitude of \(S(AB)\) and \(V(DA)\), \(B\) is a center of similitude of \(S(AB)\) and \(T(BC)\), and, as we just saw, \(P\) is a center of similitude of \(V(DA)\) and \(T(BC)\).
Relevant pages:
- The Four Touching Circles Problem
- The Four Touching Circles Problem II
- The Four Touching Circles Problem III
- The Four Touching Circles Problem IV
|Contact| |Front page| |Content| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73582971
