Napoleon's Theorem,
A Generalization

A theorem ascribed to Napoleon Bonaparte reads as follows:

On each side of a given (arbitrary) triangle describe an equilateral triangle exterior to the given one, and join the centers of the three thus obtained equilateral triangles. Show that the resulting triangle is also equilateral.

It was already pointed out that the theorem allows several generalizations. In particular, equilateral triangles can be replaced with similar triangles of arbitrary shape. This sounds even more surprising than Napoleon's theorem itself. Here I would like to consider a further generalization that makes the other two quite obvious.

	Start with two similar triangles (black). On each of the (orange) lines connecting their corresponding vertices, construct triangles (red) similar to each other and similarly oriented such that their (orange) bases correspond to each other. Then three free vertices of these triangles form a triangle similar to the original two. (See a GeoGebra illustration.)		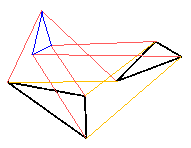(1)
	In a special case where two vertices of the given similar triangles coincide, only one (orange) line is needed to connect vertices of the two triangles. The other two pairs are connect by sides of the triangles. Three similar isosceles triangles are constructed on the vertex connecting lines.
	Changing the viewpoint, note that on the sides of ΔABC we only discern two similar triangles (thick black, on the lower two sides of ABC.) To remove this lopsidedness we construct an additional (and spurious) triangle (thin black) similar to the other two (thick black.)

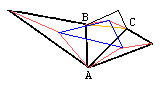
The latter illustrates the most general reformulation of the Napoleon's Theorem. The three similar triangles may be of various shapes and, in addition, one is permitted to connect any three corresponding points (and not just centroids) in order to obtain a fourth similar triangle. (On the diagram, I took the apices of similar isocseles triangles as the three corresponding points.)

(1) has a more immediate appeal than such a generalization. After all, all we did was constructing nothing but similar triangles. Having constructed a sequence of similar triangles, it seems quite "natural" to expect, as a result, another similar triangle. What else might it be?

However, (1) still requires a proof. One proof, beautiful in its generality, is based on the theory of spiral similarities. A spiral similarity is a product (or a sum, or a composition, if you will) of two plane transformations:

Rotation around a point (the center of rotation) through a fixed angle (the angle of rotation)
Central similarity (homothety with a fixed ratio and a center of homothety)

provided the centers of rotation and homothety coincide. In which case, we have a spiral similarity with a given center, a given angle, and a given ratio. Relevance of spiral similarity to (1) is based on the following intuitively acceptable fact (whose proof is, of course, left as an exercise)

If for every point of a shape F there corresponds a point of a shape F' in such a manner that corresponding segments in these figures have a constant ratio r and form a constant angle a, then F and F' are related by a central similarity with ratio r and angle α.

(There is one caveat though: if r = 1 and α = 0, we have a translation instead. In the proofs below, I disregard such a possibility. Translation is always a special case and corresponding proofs are simpler than for spiral similarity.)

Thus any two similar triangles (in particular, thick black in (1)) can be obtained from each other by a spiral similarity. Of course, rotation and homothety are particular cases of spiral similarity. Now that we began talking of rotations amid thoroughly angular constructions we dealt with so far, the following lemma may appear less surprising:

Lemma

Let there be given two circles R and R' intersecting at points M and N (The diagram on the right depicts only one possible situation.) Through M draw a line l and let A and A' denote its other points of intersection with R and R', respectively. On AA', complete a triangle AA'C similar to a given triangle GHI. As l varies, subject to the above, the locus of points C is a circle.

Proof

With a reference to a previous discussion, ANA' does not depend on the position of l. Also, all triangles ANA' are similar to each other. In particular, the ratio NA:NA' does not depend on the position of l. Therefore, A' is obtained from A by a spiral similarity with center N, angle ANA' and ratio NA:NA'. This transformation takes the circle R (the locus of points A) onto R' (the locus of points A'.)

By the same token, ANC does not depend on the position of l (because NAC does not which leads to the assertion that varying l leads to similar triangles ANC.) The ratio NA:NC does not depend on l either. Therefore, C is obtained from A by a spiral similarity with center N, angle ANC and ratio NA:NC. This similarity transforms the circle R into one traced by C. QED.

Remark

Assume in Lemma that A traces not a circle but a triangle XYZ. Circumscribing a circle around XYZ and following the proof, we see that the first transformation maps ΔXYZ into a similar triangle ΔX'Y'Z'. And, of course, the same is true for the second transformation: if A stays on ΔXYZ, the locus of points C becomes a triangle similar to ΔXYZ. This proves (1)!
The result we just proved is a formal consequence of the Fundamental Theorem of Directly Similar Figures, in which real coefficents are replaced with complex numbers. (I am grateful to Steve Gray for bringing this to my attention.)

Reference

D. Wells, You Are a Mathematician, Dover, 1970
I. M. Yaglom, Geometric Transformations, v I, MAA, 1962
I. M. Yaglom, Geometric Transformations, v II, MAA, 1968