Four Touching Circles II: What Is this About?
|
| Buy this applet What if applet does not run? |
(The circled points are draggable.)
|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|
Copyright © 1996-2012 Alexander Bogomolny
Four Touching Circles II
The applet suggests the following theorem:
| (A) | Let there be 4 circles S1, S2, S3, and S4 each tangent cyclically to its neighbors, so that S1 touches S2 and S4, S2 also touches S3, and the latter touches S4. Prove that the four tangency points are concyclic, i.e. lie on a circle. |
It has been observed that the theorem only holds when the number of external tangenices of the four circles is even. If the number of external tangenices is odd, the theorem no longer holds.
| Buy this applet What if applet does not run? |
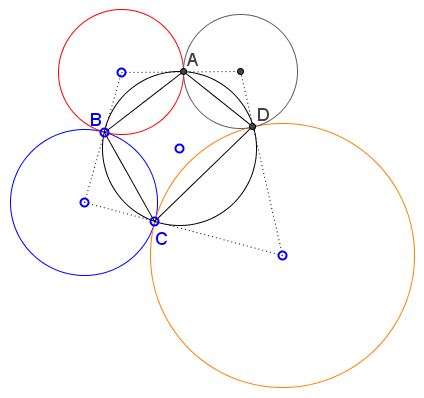
The theorem has been proved elsewhere.
The sides of the quadrilateral in question are the chords of the circles S1, S2, S3, and S4. A is the point of tangency of S1, S2, B that of S2, S3, and similar for C and D. The angles of the quadrilateral at A, B, C, D are α1, α2 and so on.
In a couple of possible configurations just testing the angles of ABCD shows that the quadrilateral is cyclic.
 |
|
}→ | α1 + α3 = α2 + α4 | ||||||||||
 |
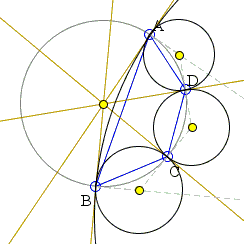| }→ | α1 + α3 = α2 + α4 | ||||||||||
 |
| }→ ? |
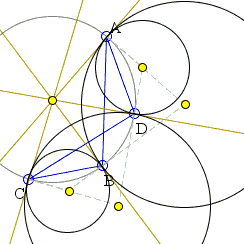where βi is the angle formed by the chord in Si and the common tangent with either Si-1 or Si+1 (the indices taken modulo 4).
In the first two cases it is obvious that
In the third case, the strategy should be changed as, otherwise, we come up with a useless identity
In the third case, we proceed as follows:
| α1 + α4 | = (-β1 + β4) + (β4 + β3) | |
| = -β1 + β3 + 2β4, | ||
| α2 + α3 | = (β2 + β1) + (β3 + β2) | |
| = β1 + 2β2 - β3. |
Now, since for the self-intersecting quadrilateral in the last diagram
|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|
Copyright © 1996-2012 Alexander Bogomolny
| 40619922 |
