The Altitudes

In a triangle, an altitude is a segment of the line through a vertex perpendicular to the opposite side. An altitude is the portion of the line between the vertex and the foot of the perpendicular. Using the standard notations, in ΔABC, there are three altitudes: AH_a, BH_b, CH_c. The three lines meet at a point - the orthocenter of the triangle. For an obtuse triangle (having one angle exceeding 90°), the orthocenter lies outside the triangle, and the segments AH_a, BH_b, CH_c do not meet. However, their extended lines do, so even in this case, it is common to assert that the altitudes are concurrent, that is pass through a point.

This is a matter of real wonderment that the fact of the concurrency of altitudes is not mentioned in either Euclid's Elements or subsequent writings of the Greek scholars. The timing of the first proof is still an open question; it is believed, though, that even the great Gauss saw it necessary to prove the fact. The earliest known proof was given by William Chapple (1718--1781). It is listed below, but appears on a separate page along with historical remarks.

---

This applet requires Sun's Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun's website at http://www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet.

---

I have collected several proofs of the concurrency of the altitudes, but of course the altitudes have plenty of other properties not mentioned below. For example, due to the mirror property the orthic triangle solves Fagnano's Problem. The foot of an altitude also has interesting properties.

1. Altitudes as Cevians
   

   This is Corollary 3 of Ceva's theorem.

2. Orthocenter as Circumcenter
   

   The orthocenter of ΔABC coincides with the circumcenter of ΔA'B'C' whose sides are parallel to those of ΔABC and pass through the vertices of the latter.

3. Orthocenter as the Isogonal Conjugate of the Circumcenter

   Besides being the bisector of angle A, l_a also bisects the angle formed by h_a and the diameter of the circumscribed circle that contains A. It follows that that diameter and h_a are isogonal images of each other. The same is true for the vertices B and C. Therefore, H is the isogonal conjugate of the circumcenter O.

4. Orthocenter as Incenter
   

   In ΔABC, ΔH_aH_bH_c is known as the orthic triangle. It has an interesting property that its angle bisectors serve in fact as altitudes of ΔABC. Thus, the fact that, in a triangle, angle bisectors are concurrent, implies the fact that altitudes in a triangle are also concurrent.

   

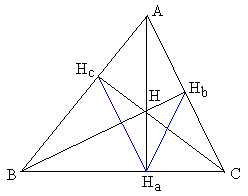
   In the proof I shall repeatedly use Euclid's Proposition III.21 about inscribed angles and its reverse. Angles BH_cC, AH_aB, AH_aC, BH_bC are all right. Therefore, we get three quadrilaterals inscribable in a circle: BH_cHH_a, BH_cH_bC, and CH_bHH_a. In each, there is a pair of equal angles. Respectively: ∠H_cBH =  ∠H_cH_aH, ∠H_cBH_b =  ∠H_cCH_b, and ∠H_bCH =  ∠H_bH_aH. It remains only to note that, naturally, ∠H_cBH =  ∠H_cBH_b and ∠H_bCH =  ∠H_bCH_c. Finally, ∠H_cH_aH = ∠H_bH_aH, which proves that H_aH is an angle bisector in the orthic triangle. The other two angles are treated similarly.

5. Via the Euler Line
   

   The argument that shows that three points - the circumcenter O, the centroid M, and the orthocenter H - lie on the same line is reversible.

   Indeed, in ΔABC consider the centroid M and the circumcenter O. If they coincide, then so are the corresponding medians and the perpendicular bisectors. In other words, the medians are perpendicular to the sides and, therefore, coincide with the altitudes. The altitudes then intersect at the centroid of the triangle (which is obviously equilateral in this case.)

   Assume that the points O and M are distinct. They define a unique line on which we'll consider a point, denoted as H, such that MH = 2·OM with M lying between O and H. Since also AM = 2·MM_a, ΔAHM is similar to ΔM_aOM. Elements VI.2 implies that lines OM_a and AH are parallel. But the former is perpendicular to BC and, therefore, so is the latter. Similarly, BH ⊥ AC and CH ⊥ AB.

6. Complex Variables
   

   A proof in the circular coordinates leads directly to the Euler line and a nice theorem by J.L.Coolidge

7. Complex Variables II
   

   Two short proofs of which the second is the clearest proof I ever came across.

8. Vector Algebra I
   

   Given ΔABC, select any point O as the origin and consider vectors OA, OB, and OC that start at O and end at the vertices of the triangle. Introduce "side" vectors: AB = OB - OA, BC = OC - OB, and AC = OC - OA. In a similar manner, other vectors will be used that lie along straight lines associated with the triangle. Assume H is the point of intersection of AH_a and BH_b. Then AH ⊥ BC and BH ⊥ AC. The scalar product of orthogonal vectors is 0. We thus have two equations

   (OH - OA).(OC - OB) = 0 and (OH - OB).(OC - OA) = 0

   Subtract the first equation from the second, multiply out and simplify:

   OH.OB + OA.OC - OB.OC - OH.OA = (OH - OC).(OB - OA) = CH.AB = 0

   Therefore CH ⊥ AB. Thus the third altitude CH_c passes through the point of intersection of the first two.

9. Vector Algebra II
   

   Let now O be the circumcenter of ΔABC. Define H via OH = OA + OB + OC. We are going to show that H lies on each of the altitudes of ΔABC. For example,

   AH.BC	= (AO + OH).(BO + OC)
   	= (-OA + OA + OB + OC).(OC - OB)
   	= (OB + OC).(OC - OB)
   	= OC.OC - OB.OB
   	= OC² - OB²
   	= 0,

   because O is the circumcenter of ΔABC.

10. Elementary Geometry, Inscribed Angles
    

    Thanks to Bianco for this proof. See also Altshiller-Court's College Geometry, p. 94.

    Let H be the point of intersection of two altitudes BH_b and CH_c. We are going to prove that the line AH is perpendicular to BC.

    The quadrilateral CH_bH_cB is cyclic. Indeed, since the angles at H_b and H_c are right, the quadrilateral is inscribed in the circle with diameter on BC. From here, ∠BCH_c = ∠BH_bH_c. On the hand, the quadrilateral AH_bHH_c is also cyclic, as the circle with diameter AH passes through all four points. Therefore, ∠HH_bH_c = ∠HAH_c. Combining the two equalities, we get ∠BCH_c = ∠HAH_c.

    Extend AH beyond H. Let G be the point of intersection of AH and BC. In triangles CHG and AHH_c, ∠GCH = ∠HAH_c and also ∠CHG = ∠AHH_c. The triangles are therefore similar. Which implies that ∠HGC = ∠HH_cA = 90° making CG the third altitude.

11. Plain Analytic Geometry
    

    (Vladimir Zajic.) Assume a triangle ABC in a carthesian coordinate system. Assume that no side is parallel to any of the 2 coordinate axes (x, y). If yes, we can always rotate the coordinate system by an arbitrary angle different from all triangle interior angles. Since the coordinate axes x, y are perpendicular to each other and since each altitude is perpendicular to one side, it follows that no altitude is parallel to any coordinate axis either. Let the coordinates of the 3 vertices be:

    A = (x_A, y_A)
    B = (x_B, y_B)
    C = (x_C, y_C).

    Equations of the 3 side lines are

    c = AB: y - yA = {(yA - yB)· x + xA· yB - xB· yA} / (xA - xB) a = BC: y - yB = {(yB - yC)· x + xB· yC - xC· yB} / (xB - xC) b = CA: y - yC = {(yC - yA)· x + xC· yA - xA· yC} / (xC - xA)

    We have to calculate only 1 equation, the other 2 are given by cyclic permutation of indices A, B, C.

    Lemma

    Two lines (none parralel to any coordinate axis) are perpendicular to each other if and only if the product of their tangents is equal to -1 (minus one).

    Equations of the 3 altitudes CH_c, BH_c, AH_a are obtained by using the tangents of the side lines, the lemma, and the fact that they pass through the corresponding vertex. Again, we have to set up only 1 equation, the other 2 are given by the cyclic permutation of A, B, C.

    CH_c: y - y_C = {-(x_A - x_B)· x + (x_A - x_B)· x_C} / (y_A - y_B)

    AH_a: y - y_A = {-(x_B - x_C)· x + (x_B - x_C)· x_A} / (y_B - y_C)

    BH_b: y - y_B = {-(x_C - x_A)· x + (x_C - x_A)· x_B} / (y_C - y_A)

    To find the coordinates of the intersect (the orthocenter), take any two altitude equations and solve for x and y. For example, CH_c x BH_b:

    x_O = {x_A· x_B· (y_A - y_B) + x_B· x_C· (y_B - y_C) + x_C· x_A· (y_C - y_A) - (y_A - y_B)· (y_B - y_C)· (y_C - y_A)}
    / (x_C· y_B - x_B· y_C + x_A· y_C - x_C· y_A + x_B· y_A - x_A· y_B)

    y_O = {y_A· y_B· (x_A - x_B) + y_B· y_C· (x_B - x_C) + y_C· y_A· (x_C - x_A) - (x_A - x_B)· (x_B - x_C)· (x_C - x_A)}
    / (y_C· x_B - y_B· x_C + y_A· x_C - y_C· x_A + y_B· x_A - y_A· x_B)

    Since the solution is invariant with respect to the cyclic permutation of A, B, C, it follows that the same coordinates x_O and y_O are solution of any two altitude coordinates and the 3 altitudes indeed intersect in a single point. This could be also verified by a direct solution of all altitude equation pairs.

12. Plane Geometry
    

    (Vladimir Zajic.) Assume a ΔABC, the side c = AB is horizontal, the vertex C is above. Extend the sides a = BC and b = CA upwards beyond the vertex C.

    Construct the altitudes h_a and h_b by dropping normals from the vertices A and B to the opposite sides a = BC and b = CA, respectively. Denote O the intersection of these two altitudes. Denote H_a and H_b the heels of the altitudes h_a and h_b, respectively (i.e., their intersections with the corresponding triangle sides).

    Construct the altitude h_c of the ΔABO by dropping a normal from the vertex O to the side c = AB. Denote H_c the heel of this altitude. Extend the altitude h_c of the ΔABO upwards until it intersects both the (extended) lines a = BC and b = CA. Suppose that these intersections might be different from each other (see the attached drawing). Denote the intersections C_a and C_b, respectively. Then either OC_a < OC_b or OC_a > OC_b.

    

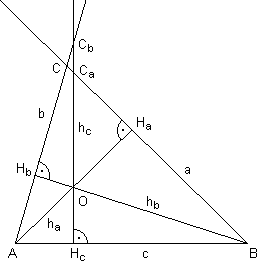
    Note that the following triangle pairs are similar (because both triangles in each pair have the same angles at the vertex O and each triangle has a right angle):

    ΔAOH_b and ΔBOH_a

    ΔAOH_c and ΔC_aOH_a

    ΔBOH_c and ΔC_bOH_b

    Consequently

    OA/OH_b = OB/OH_a

    OA/OH_c = OC_a/OH_a

    OB/OH_c = OC_b/OH_b

    Eliminating OA and OH_a by dividing the left sides and the right sides of the first two equations we get

    OH_c/OH_b = OB/OC_a

    Multiplying the left sides and the right sides of the result and of the third equation eliminates almost everything else:

    OB/OH_b = OC_b/OH_b· OB/OC_a

    OC_b/OC_a = 1

    The line segments OC_b and OC_a are equal. In other words, the lines a and b intersect on the normal h_c to the line c dropped from the point O and the points C, C_b, and C_a are identical. Q.E.D.

13. Altitudes As Radical Axes
    

    

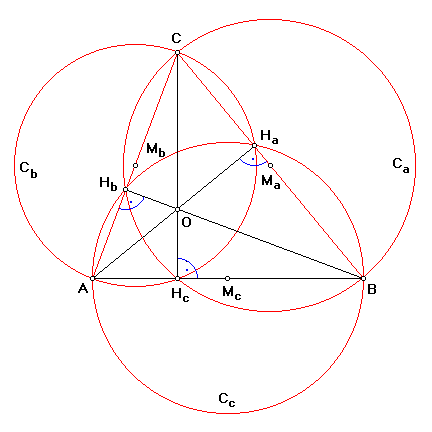
    (Vladimir Zajic.) Form three circles C_a, C_b, and C_c on the sides BC, AC, and AB of ΔABC as diameters. Circles C_a and C_b meet at C and one other point. This point lies on AB and is in fact the foot H_c of the altitude CH_c. Indeed, let K be the point of intersection (other than B) of C_a with AB. Then ∠CKB = 90°, so that CK is perpendicular to AB. Therefore K = H_c. Similarly, circle C_b meets AB at H_c (and, of course, A.) We conclude that two circles C_a and C_b that obviously meet at C, also meet at H_c. CH_c is therefore the radical axis of the two circles.

    Turning to other sides and pairs of circles, we see that the altitudes of ΔABC serve as radical axes of the circles C_a, C_b, and C_c taken in pairs. As we know, the pairwise radical axes of three circles concur in a point, and so do the three altitudes of a triangle.

    (A more general statement appears as Theorem 184 in A Treatise On the Circle and the Sphere by J. L. Coolidge: The orthocenter of a triangle is the radical center of any three circles each of which has a diameter whose extremities are a vertex and a point on the opposite side line, but no two passing through the same vertex. The proof is practically the same.)

14. Via Carnot's Theorem
    

    The identity

    (1)	AC'² - BC'² + BA'² - CA'² + CB'² - AB'² = 0.

    in Carnot's theorem is easily verified when AA', BB', CC' are the altitudes of ΔABC.

15. A Proof from 1749
    

    A former correspondent sent me a surprise note (Jan 20, 2010):

    Here is William Chapple's demonstration that the altitudes of a triangle are coincident. It comes from the Miscellanea Curiosa Mathematica, Number IX, edited by Francis Holliday and published by Cave - I understand that this publication was launched in 1745, with two issues a year, which would place the publication date in 1749, the year of publication of a collected edition ...

    William Chapple's demonstration refers to the following diagram:

    

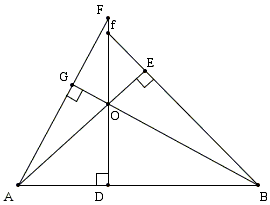
    I placed the proof itself on a separate page along with a commentary by Thomas Stephens Davies in The Philosophical Magazine in 1850.

16. And a More Recent Proof
    

    This proof is due to V. Nikolin, an elementary school teacher from Serbia, and is based on the following diagram:

    

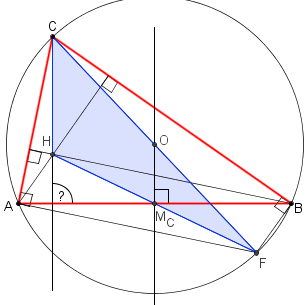
    The short proof is available on a separate page.

17. Lightened Analytic Proof
    

    This and the next 3 proofs are due to Michel Cabart (Feb 1, 2011).

    

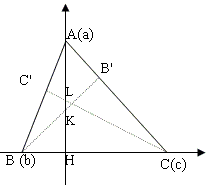
    Let's take as x-axis the side BC and as y-axis the altitude AH, so that the origin is H. The coordinates are A(0, a), B(b, 0) and C(c, 0). We want to show that intersections L and K have same ordinate. Slope of (AB) is -a/b hence slope of (CC') is b/a and equation of (CC') is

    y = (b/a)·(x - c) = (b/a)x -(bc/a).

    Thus ordinate of K is (-bc/a). This is symmetric in b and c, so we are sure to find the same result for L.

18. Short Geometric Proof
    

    With a reference to the diagram in the previous proof, triangles AHB and CHL are similar (rectangle triangles with ∠HAB = ∠HCL), thus HB·HC = HA·HL. By symmetry (or considering triangles AHC and BHK) we get HB·HC = HA·HK. Hence HK = HL and K = L.

19. Classic vector proof
    

    Euler's identity says: MA·BC + MB·CA + MC·AB = 0 (scalar product). Thus if M is the intersection of altitudes from A and B, the first two terms vanish, hence, also the third one, which yields the result.

20. Projective Proof (Chasles)
    

    Let's consider the quadrilater HABC in this order, H being any point.

    

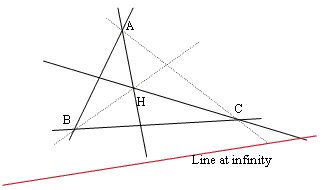
    From Desargues' theorem, the line at infinity cuts (AB) and (CH), (AC) and (BH), (BC) and (AH) in three pairs of points in involution: C' - H1, B' - H2, A' - H3. If two pairs of lines are perpendicular, the double points of the involution are the cyclic points. Then the third pair of lines is also perpendicular.

1. N. Altshiller-Court, College Geometry, Dover, 1980
2. J. L. Coolidge, A Treatise On the Circle and the Sphere, AMS - Chelsea Publishing, 1971
3. H. S. M. Coxeter, S. L. Greitzer, Geometry Revisited, MAA, 1967
4. H. S. M. Coxeter, Introduction to Geometry, John Wiley & Sons, 1961
5. D. Pedoe, Geometry: A Comprehensive Course, Dover, 1970
6. V. V. Prasolov, Essays on Numbers and Figures, AMS, 2000

|Contact| |Front page| |Contents| |Geometry| |Store|

Copyright © 1996-2012 Alexander Bogomolny