Two Colors - Three Points

Points in the plane are colored in two colors. Prove that it is always possible to find a monochromatic equilateral triangle, i.e., three points of the same color with all pairwise distances equal.

Solution

|Contact| |Front page| |Contents| |Coloring Plane| |Store|

Copyright © 1996-2015 Alexander Bogomolny

Points in the plane are colored in two colors. Prove that it is always possible to find a monochromatic equilateral triangle, i.e., three points of the same color with all pairwise distances equal.

For convenience, name the colors red and blue.

Start with finding three collinear points A, B, C of the same color. Add points D, E, F as shown:

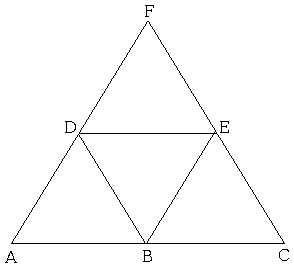
There are 1 big and 4 small equilateral triangles. Assume A, B, C are red. If one of D or E is red, we are done. Otherwise, they both are blue. Then if F is red, triangle ACF is monochromatic. Otherwise, if F is blue, triangle DEF is monochromatic.

References

1. R. B. J. T. Allenby, A. Slomson, How to Count: An Introduction to Combinatorics, CRC Press, 2011 (2nd edition)

1. Ramsey's Theorem
2. Party Acquaintances
3. Ramsey Number R(3, 3, 3)
4. Ramsey Number R(4, 3)
5. Ramsey Number R(5, 3)
6. Ramsey Number R(4, 4)
7. Geometric Application of Ramsey's Theory
8. Coloring Points in the Plane and Elsewhere
9. Two Colors - Two Points
10. Three Colors - Two Points
11. Two Colors - All Distances
12. Two Colors on a Straight Line
13. Two Colors - Three Points
14. Three Colors - Bichromatic Lines
15. Chromatic Number of the Plane
16. Monochromatic Rectangle in a 2-coloring of the Plane
17. Two Colors - Three Points
18. Coloring a Graph
19. No Equilateral Triangles, Please

|Contact| |Front page| |Contents| |Coloring Plane| |Store|

Copyright © 1996-2015 Alexander Bogomolny