Three Complex Numbers Satisfy Fermat's Identity For Prime Powers

Problem

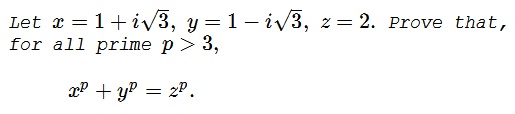
Solution 1

Not that $x^6=y^6=2^6=z^6.$ Also, $x+y=2=z$ and $\displaystyle \frac{1}{x}+\frac{1}{y}=\frac{1}{2}=\frac{1}{z}.$

Now, all prime numbers are in the form $p=6m\pm 1.$ Assume $p=6m+1.$ Then

$\begin{align} x^{p}+y^{p}&=x\cdot x^{6m}+y\cdot y^{6m}=x\cdot (x^6)^m+y\cdot (y^6)^m\\ &=2^{6m}(x+y)=2^{6m+1}=2^p\\ &=z^p. \end{align}$

For $p=6m-1$ the derivation is practically the same:

$\displaystyle \begin{align} x^{p}+y^{p}&=\frac{1}{x}\cdot x^{6m}+\frac{1}{y}\cdot y^{6m}=\frac{1}{x}\cdot (x^6)^m+\frac{1}{y}\cdot (y^6)^m\\ &=2^{6m}(\frac{1}{x}+\frac{1}{y})=2^{6m}\cdot\frac{1}{2}=2^{6m-1}=2^p\\ &=z^p. \end{align}$

Solution 2

$\displaystyle \begin{align} f&=\left(\frac{x}{2}\right)^p+\left(\frac{y}{2}\right)^p=\left(\frac{1}{2}+i\frac{\sqrt{3}}{2}\right)^p+\left(\frac{1}{2}-i\frac{\sqrt{3}}{2}\right)^p\\ &=\exp\left(\frac{ip\pi}{3}\right)+\exp\left(\frac{-ip\pi}{3}\right)\\ &=2\cos\frac{p\pi}{3}. \end{align}$

Every prime greater than $3$ is of the form $6k+1$ or $6k-1$ where $k$ is a positive integer. Thus,

$\displaystyle f=2\cos\left(2k\pi\pm\frac{\pi}{3}\right)=2\cos\left(\frac{\pi}{3}\right)=1.$

Acknowledgment

The problem came from Ross Honsberger's Mathematical Morsels, (MAA, 1978, #20). Honsberger refers to problem E518 from AMM (1943), p. 63. Solved by J. Rosenbaum, CT.

Solution 2 is by Amit Itagi.

Remark

It must be noted that the above solutions work for all $6m\pm 1,$ $m\ge 1,$ not necessarily prime. Thus the imposition that $p$ needs to be a prime is a diversion and, therefore, a red herring.

What Is Red Herring

72182677