An Inequality from the 2015 Romanian TST

This is Problem 2 from the 2015 Romanian TST (Team Selection Test) seniors. It has been posted at the CutTheKnotMath facebook page by Leo Giugiuc along with his own and an unnamed student solution. I reproduce the latter below and link to Leo's solution. The problem is due to Professor Dorin Andrica.

Let $r$ be the inradius of $\Delta ABC.$ Form circles $(O_a),(O_b),(O_c)$ tangent to the circumcircle $(ABC)$ at the vertices $A,B,C,$ respectively, and tangent to the sides opposite the corresponding vertices. The radii of the circles are denoted $R_a,R_b,R_c,$ respectively.

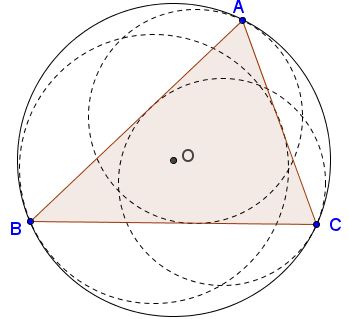
Dorin Andrica's problem, problem

Prove that

$\displaystyle \frac{1}{R_a}+\frac{1}{R_b}+\frac{1}{R_c}\le \frac{2}{r}.$

Proof

It is known that, for $h_a,h_b,h_c$ the (lengths of the) altitudes in $\Delta ABC,$

$\displaystyle \frac{1}{h_a}+\frac{1}{h_b}+\frac{1}{h_c}= \frac{1}{r}.$

The center of a circle tangent to a circumcircle of a triangle at a vertex lies on the line joining that vertex with the circumcenter. If in addition, it is tangent to the opposite side, its center is equidistant from the vertex and the side. E.g., consider $(O_a):$

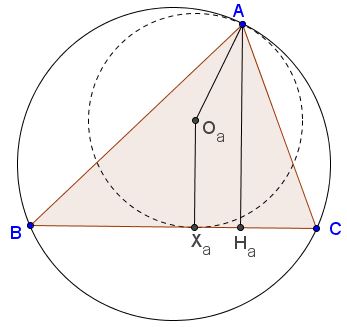
Dorin Andrica's problem, solution

Let $H_a,X_a$ be the feet of the perpendiculars from $A$ and $O_a$ to $BC:$ $AH_a=h_a,$ $O_aX_a=AO_a=R_a.$ It follows that $2R_a\ge h_a.$ In other words, $\displaystyle\frac{1}{2R_a}\le\frac{1}{h_a}.$ The same holds for other vertices. Adding up the three inequalities gives:

$\displaystyle\frac{1}{2R_a}+\frac{1}{2R_b}+\frac{1}{2R_c}\le\frac{1}{h_a}+\frac{1}{h_b}+\frac{1}{h_c}=\frac{1}{r}.$

Note that the requirement for the circles to be tangent to the circumcircle is a red herring: the required inequality holds for any triple of circles tangent to the sides and through the opposite vertex. The equality holds only when all three have the altitudes as their diameters.

What Is Red Herring

71876480