Circle through the Incenter And Antiparallels
The applet below illustrates problem 7 from the 2009 Australian Mathematical Olympiad.
Let I be the incenter of a triangle ABC in which AC ≠ BC. Let Γ be the circle passing through A, I and B. Suppose Γ intersects the line AC at A and X and intersects the line BC at B and Y . Show that AX = BY.
The condition AC ≠ BC is obviously a red herring as, in this case,
| Buy this applet What if applet does not run? |
|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|
Copyright © 1996-2015 Alexander Bogomolny
Let I be the incenter of a triangle ABC in which AC ≠ BC. Let Γ be the circle passing through A, I and B. Suppose Γ intersects the line AC at A and X and intersects the line BC at B and Y . Show that
| Buy this applet What if applet does not run? |
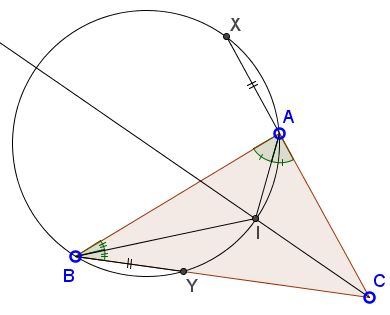
This is a well known fact that a circle through two vertices of a triangle cuts a chord (XY in the applet) antiparallel to the side joining the two vertices (AB in the applet).
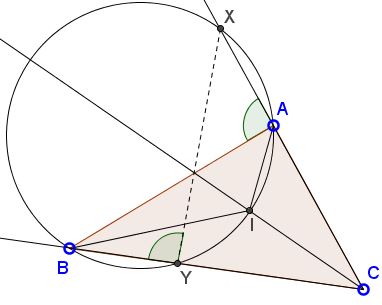
In particular this means that ∠BAX = ∠BYX. These angles are subtended by the arcs BXA and YBX. For the arcs (depending on the layout and assuming J is the second point of intersection of the circle with CI), either
| BXA | = BJX + XA, | |
| YBX | = YB + BJX, |
or
| BXA | = BIX + XA, | |
| YBX | = YB + BIX. |
In both cases the arcs XA and YB are equal, implying the identity of the subtended chords.
There are five solutions in all:
Red Herrings: a Sample List
- On the Difference of Areas
- Area of the Union of Two Squares
- Circle through the Incenter
- Circle through the Incenter And Antiparallels
- Circle through the Circumcenter
- Inequality with Logarithms
- Breaking Chocolate Bars
- Circles through the Orthocenter
- 100 Grasshoppers on a Triangular Board
- Simultaneous Diameters in Concurrent Circles
- An Inequality from the 2015 Romanian TST
- Schur's Inequality
- Further Properties of Peculiar Circles
|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|
Copyright © 1996-2015 Alexander Bogomolny
| 49551914 |
