Mickey Might Be a Red Herring in the Mickey Mouse Theorem
What Is This About?
Source

Problem
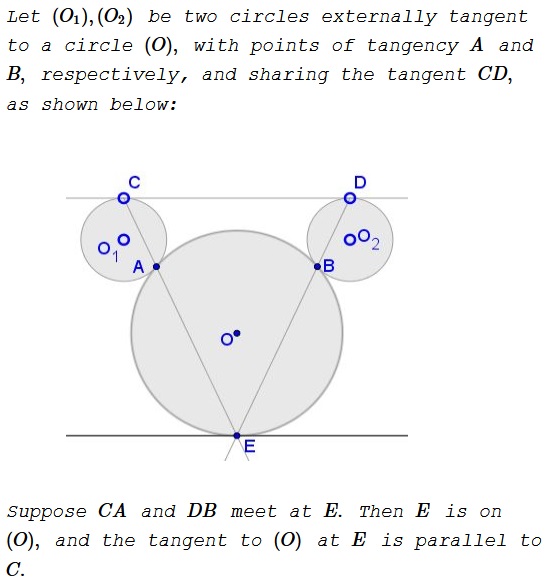
Solution
For a proof we only need two circles, say $(O_1)\,$ and $(O).\,$ Let $CA\,$ crosses $(O)\,$ the second time at $E.\,$ Then triangles $AO_1C\,$ and $AOE\,$ are isosceles and, since $\angle CAO_1=\angle EAO,\,$ it also follows that $\angle O_1CA=\angle OEA.$
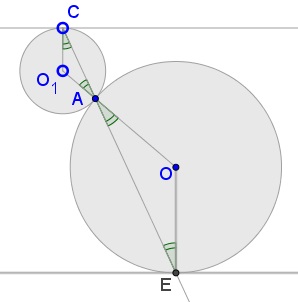
Thus, $CO_1\parallel OE\,$ and, since $CO_1\,$ is perpendicular to the tangent to $(O_1)\,$ at $C,\,$ the same is true of $OE.\,$ But $OE\,$ is also perpendicular to the tangent to $(O)\,$ at $E,\,$ thus, implying that the two tangents are parallel.
We can say that $E\,$ lies on the perpendicular to the tangent at $C\,$ through $(O).\,$ Since originally, $(O_1)\,$ and $(O_2)\,$ share that tangent $CD,\,$ $DB\,$ necessarily passes through $E\,$ so that indeed $CA\,$ and $DB\,$ meet on $(O).\,$
Remark
From the above proof it is clear that the presence of two Mickey Mouse ears in the theorem, while entertaining, is not essential. The basic result only deals with one circle $(O_1)\,$ whereas the statement remains true for any number of circles $(O_2),\,$ $(O_3),\ldots,\,$ simultaneously tangent to $(O)\,$ and to a selected tangent to $(O_1).\,$
This opens a door to consider the second ear and, thus Mickey Mouse himself, as a red herring in the eponymous theorem.
What Is Red Herring
- On the Difference of Areas
- Area of the Union of Two Squares
- Circle through the Incenter
- Circle through the Incenter And Antiparallels
- Circle through the Circumcenter
- Inequality with Logarithms
- Breaking Chocolate Bars
- Circles through the Orthocenter
- 100 Grasshoppers on a Triangular Board
- Simultaneous Diameters in Concurrent Circles
- An Inequality from the 2015 Romanian TST
- Schur's Inequality
- Further Properties of Peculiar Circles
- Inequality with Csc And Sin
- Area Inequality in Trapezoid
- Triangles on HO
- From Angle Bisector to 120 degrees Angle
- A Case of Divergence
- An Inequality for the Cevians through Spieker Point via Brocard Angle
- An Inequality In Triangle and Without
- Problem 3 from the EGMO2017
- Mickey Might Be a Red Herring in the Mickey Mouse Theorem
- A Cyclic Inequality from the 6th IMO, 1964
- Three Complex Numbers Satisfy Fermat's Identity For Prime Powers
- Probability of Random Lines Crossing
- Planting Trees in a Row
- Two Colors - Three Points
Acknowledgment
The problem was posted by Takis Chronopoulos at the Romantics of Geometry (Οι Ρομαντικοι της Γεωμετριας) facebook group.
![]()
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73606874
