An Inequality In Triangle and Without
Problem
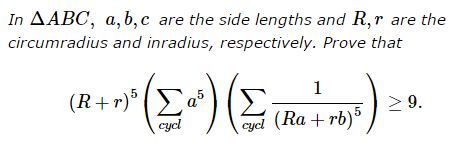
Solution 1
By Hölder's inequality,
$\displaystyle\begin{align} \left(\sum_{3\,times}(R+r)^5\right)\left(\sum_{cycl}a^5\right)&(1+1+1)(1+1+1)(1+1+1)\\ &\ge [(Ra+ra)+(Rb+rb)+(Rc+rc)]^5. \end{align}$
It follows that
(A)
$\displaystyle 3(R+r)^5\left(\sum_{cycl}a^5\right)\cdot 27\ge [(Ra+rb)+(Rb+rc)+(Rc+ra)]^5.$
On the other hand, by the AM-GM inequality,
(B)
$\displaystyle [(Ra+rb)+(Rb+rc)+(Rc+ra)]^5\left(\sum_{cycl}\frac{1}{(Ra+rb)^5}\right)\ge 729.$
because
$\displaystyle [(Ra+rb)+(Rb+rc)+(Rc+ra)]^5\ge 3^5\sqrt[3]{\left((Ra+rb)(Rb+rc)(Rc+ra)\right)^5},$
whereas
$\displaystyle \sum_{cycl}\frac{1}{(Ra+rb)^5}\ge 3\frac{1}{\sqrt[3]{\left((Ra+rb)(Rb+rc)(Rc+ra)\right)^5}},$
The product of (A) and (B) is exactly the required inequality.
Solution 2
(1)
$\displaystyle \sum_{cycl}\frac{1}{(Ra+rb)^5}\ge \frac{(1+1+1)^6}{\displaystyle \sum_{cycl}(Ra+rb)^5}.$
Now,
$\displaystyle\begin{align} \sum_{cycl}(Ra+rb)^5 &\lt (Ra+rb+Rb+rc+Rc+ra)^5\\ &=(R\sum_{cycl}a+r\sum_{cycl}a)^5=(R+r)^5\left(\sum_{cycl}a\right)^5. \end{align}$
It follows that
(2)
$\displaystyle \frac{1}{\displaystyle \sum_{cycl}(Ra+rb)^5}\gt \frac{1}{\displaystyle(R+b)^5\left(\sum_{cycl}a\right)^5}.$
Combining (1) and (2),
$\displaystyle \frac{1}{\displaystyle \sum_{cycl}(Ra+rb)^5}\gt \frac{(1+1+1)^6}{\displaystyle \sum_{cycl}(Ra+rb)^5}.$
Thus, using Chebyshev's inequality,
$\displaystyle\begin{align} LHS &= (R+r)^5\left(\sum_{cycl}a^5\right)\left(\sum_{cycl}\frac{1}{(Ra+rb)^5}\right)\\ &\gt\frac{\displaystyle 3^6\left(\sum_{cycl}a^5\right)}{\displaystyle\left(\sum_{cycl}a\right)^5}\ge\frac{\displaystyle 3^6\cdot\frac{1}{3^4}\left(\sum_{cycl}a\right)^5}{\displaystyle\left(\sum_{cycl}a\right)^5}\\ &=9=RHS. \end{align}$
The inequality is strict.
Acknowledgment
Kevin Soto Palacios (Peru) has kindly posted at the CutTheKnotMath facebook page his solution to a problem he credits to Dan Sitaru. Solution 2 is by Soumava Chakraborty.
As Kevin solution shows, the inequality has little to do with the triangle or its associated radii. It is true in a rectified formulation:
Let $a, b, c,s,t\,$ be positive real numbers. Prove that
$\displaystyle (s+t)^5\left(\sum_{cycl}a^5\right)\left(\sum_{cycl}\frac{1}{(sa+tb)^5}\right)\ge 9.$
I find this a most cleverly conceived occurrence of the Red Herring.
What Is Red Herring
- On the Difference of Areas
- Area of the Union of Two Squares
- Circle through the Incenter
- Circle through the Incenter And Antiparallels
- Circle through the Circumcenter
- Inequality with Logarithms
- Breaking Chocolate Bars
- Circles through the Orthocenter
- 100 Grasshoppers on a Triangular Board
- Simultaneous Diameters in Concurrent Circles
- An Inequality from the 2015 Romanian TST
- Schur's Inequality
- Further Properties of Peculiar Circles
- Inequality with Csc And Sin
- Area Inequality in Trapezoid
- Triangles on HO
- From Angle Bisector to 120 degrees Angle
- A Case of Divergence
- An Inequality for the Cevians through Spieker Point via Brocard Angle
- An Inequality In Triangle and Without
- Problem 3 from the EGMO2017
- Mickey Might Be a Red Herring in the Mickey Mouse Theorem
- A Cyclic Inequality from the 6th IMO, 1964
- Three Complex Numbers Satisfy Fermat's Identity For Prime Powers
- Probability of Random Lines Crossing
- Planting Trees in a Row
- Two Colors - Three Points
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny
73579887
