Triangles on HO

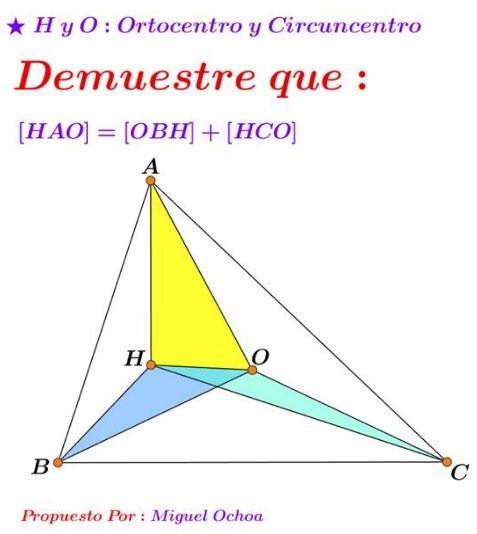
The problem has been shared by Miguel Ochoa Sanchez at the Peru Geometrico facebook group.

As stated, the problem is incorrect: It is not always true that $[\Delta AHO]=[\Delta BHO]+[\Delta CHO].\,$ The suspicion may be aroused by the lack of symmetry in the formulation: both the orthocenter $H\,$ and the circumcenter $O\,$ are symmetric functions of the vertices of $\Delta ABC.\,$ There is no reason to single out one of the vertices. The improved formulation is as follows:

The problem, as stated above, appears somewhat artificial. Let $h_A,\,$ $h_B,\,$ $h_C,\,$ be the altitudes of the three triangle involved to the line $HO.\,$ Since all three have the same base $(HO)\,$ the problem reduce to proving that

$h_A+h_B+h_C=0.$

(This in fact explains the idea of signed areas: depending on the position of the vertices relative to the line $HO,\,$ the altitudes may be either positive or negative.)

Remarkably, the above condition does not depend on the specific common base of the three triangles. As the line $HO\,$ is the Euler line of $\Delta ABC,\,$ it is obvious that for any two points $P,Q\,$ on the Euler line we'll have

$[APQ]+[BPQ]+[CPQ]=0.$

Thus, inclusion of $H\,$ and $O\,$ in the formulation is a red herring. But this is not the only red herring in the formulation. What makes the Euler line so special as to possess such a nice property? To make sure, the Euler line is a very special construct in every triangle, but the condition $h_A+h_B+h_C=0\,$ seems too general to be strictly and rigidly associated with the Euler line. Indeed, if we imagine unit masses placed on the vertices of the triangles, the equation $h_A+h_B+h_C=0\,$ will simply assert that the moments of the system of three masses with respect to $HO\,$ is zero, i.e., the system is in equilibrium. This observation removes the mystery in the appearance of the Euler line. The Euler line passes through $H,\,$ $O,\,$ but - in this case - more importantly - through $G,\,$ the centroid, i.e., the barycenter of the triangle. For every line though the centroid of $\Delta ABC,\,$ the required condition will hold!