Concurrence in Arbelos
What is this about?
Problem
Consider arbelos formed by the semicircles $(AB),$ $(AC),$ and $(BC),$ as shown. Let $D,E,F$ be the midpoints of the arcs. Assume $C(X,Y)$ denotes the circle centered at $X$ and passing through $Y.$
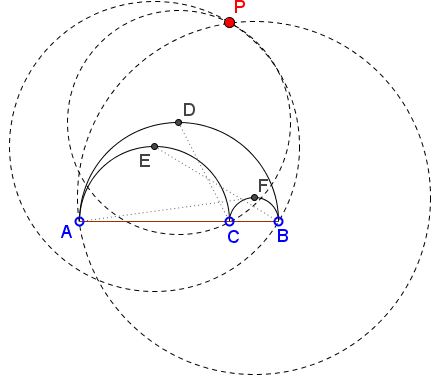
Then circles $C(D,C),$ $C(E,B),$ and $C(F,A)$ are concurrent.
Proof 1
This is a straightforward solution that I came up with without having a good look at the diagram.
Let $K,L,O$ be the centers of $(AC),$ $(BC),$ and $(AB),$ respectively; denote their radii as $r_{k},$ $r_{l},$ and $r_{o}.$ Note that $r_o=r_{k}+r_{i}.$ Assume without loss of generality that $r_{k}\ge r_{l}.$
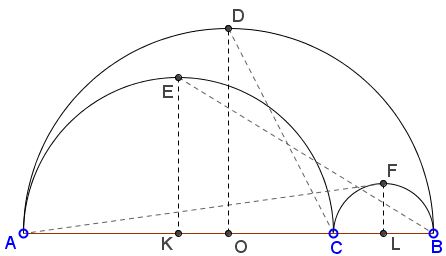
First we determine the radii of the three circles $C(D,C),$ $C(E,B),$ $C(F,A).$
In the right $\Delta CDO,$
$DO=r_{o}=r_{k}+r_{l},\\ CO=BO-BC=r_{o}-2r_{l}=r_{k}-r_{l},$
implying $DC^{2}=DO^{2}+CO^{2}=2(r_{k}^{2}+r_{l}^{2}).$
Similarly, from the right triangles $AFL$ and $BEK,$
$AF^{2}=(2r_{k}+r_{l})^{2}+r_{l}^{2},\\ BE^{2}=(r_{k}+2r_{l})^{2}+r_{k}^{2}.$
If we choose $C$ as the origin of the Euclidean system, $E=(-r_{k},r_{k}),$ $F=(r_{l},r_{l}),$ and $D=(r_{l}-r_{k},r_{k}+r_{l}).$ Thus we have three circles:
$\begin{align} C(D,C):& (x-(r_{k}-r_{l}))^{2}+(y-(r_{k}+r_{l}))^{2}=2(r_{k}^{2}+r_{l}^{2}),\\ C(E,B):& (x+r_{k})^{2}+(y-r_{k})^{2}=(r_{k}+2r_{l})^{2}+r_{k}^{2},\\ C(F,A):& (x-r_{l})^{2}+(y-r_{l})^{2}=(2r_{k}+r_{l})^{2}+r_{l}^{2}. \end{align}$
The circle equations simplify to
$\begin{align} C(D,C):& x^{2}-2x(r_{k}-r_{l})+y^{2}-2y(r_{k}+r_{l})=0,\\ C(E,B):& x^{2}+2xr_{k}+y^{2}-2yr_{k}=4r_{k}r_{l}+4r_{l}^{2},\\ C(F,A):& x^{2}-2xr_{l}+y^{2}-2yr_{l}=4r_{k}^{2}+4r_{k}r_{l}. \end{align}$
Subtracting the first equation from the other two gives two linear equations:
$x(2r_{k}-r_{l})+yr_{l}=2r_{k}r_{l}+2r_{l}^{2}\\ x(r_{k}-2r_{l})+yr_{k}=2r_{k}^{2}+2r_{k}r_{l}.$
Now, multiply the first of these by $r_{k},$ the second by $r_{l}$ and subtract:
$x(r_{k}^{2}-r_{k}r_{l}+r_{l}^{2})=0.$
From which $x=0.$ Substituting this into the equation of say, $C(D,C)$ gives $y=0$ and $y=2(r_{k}+r_{l}).$ The former should be discarded as the point $(0,0)$ belongs only to $C(D,C)$ and not to the other two circles. However point $(0,2(r_{k}+r_{l}))$ belongs to all three.
Proof 2
Construct square $ABHI$ on the same side as the arbelos. Let $P$ on the upper edge of the square such that $CP\perp AB.$ Note that $D$ is the center of the square so that $CD=DP,$ implying that $P$ lies on $C(D,C).$
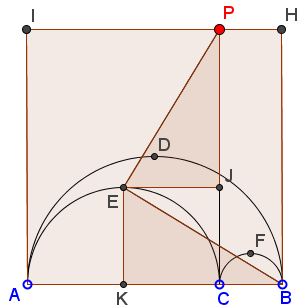
Let $K$ be as before, the center of $(AC)$ and $J$ on $CP$ such that $EJ\perp CP.$ Since $CJEK$ is a square, the right triangles $BEK$ and $PEJ$ are equal, showing that also $BE=EP$ such that $P$ belongs to $C(E,B).$ Similarly, it also lies on $C(F,A).$
Acknowledgment
Emmanuel Antonio José García (Dominican Republic) posted his discovery of the concurrence at the CutTheKnotMath facebook page with a link to the Advanced Euclidean Geometry yahoo group, where Paul Yiu posted the elegant geometric solution I used above (Proof 2).
There could not be two opinions which proof is shorter, easier to follow through, more enlightening. I added the first proof so that it would be possible to make that point. Even, if you came up with something like Proof 1, the final result for the common point $P(0,2(r_{k}+r_{l}))$ should sound an alert that would warrant having a look back for, after all, $AB=2(r_{k}+r_{l}).$
- Arbelos - the Shoemaker's Knife
- 7 = 2 + 5 Sangaku
- Another Pair of Twins in Arbelos
- Archimedes' Quadruplets
- Archimedes' Twin Circles and a Brother
- Book of Lemmas: Proposition 5
- Book of Lemmas: Proposition 6
- Chain of Inscribed Circles
- Concurrency in Arbelos
- Concyclic Points in Arbelos
- Ellipse in Arbelos
- Gothic Arc
- Pappus Sangaku
- Rectangle in Arbelos
- Squares in Arbelos
- The Area of Arbelos
- Twin Segments in Arbelos
- Two Arbelos, Two Chains
- A Newly Born Pair of Siblings to Archimedes' Twins
- Concurrence in Arbelos
- Arbelos' Morsels
![]()
|Contact| |Front page| |Contents| |Geometry| |Up|
Copyright © 1996-2018 Alexander Bogomolny73583451
