Squares in Arbelos

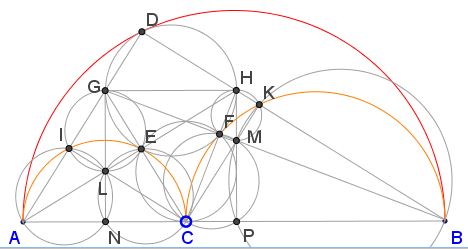
Arbelos is a shape made famous by Archimedes with its inclusion in his Book of Lemmas. Three lemmas from the surviving 15 deal with arbelos. Arbelos is bounded by three touching semicircles two of whose diameters combine into a diameter of the third. Lemma 6 describes the properties of an Apollonian circle tangent to the three arcs of an arbelos.

Curiously, a feature of the diagram that is a consequence of well known properties has not, to the best of my knowledge, been mentioned explicitly.

It was observed by Greg Markowsky (2007) that, enmeshed in the diagram, one may discern two squares: NPHG and CKDI. Prove that, indeed, the two quadrilaterals are squares. (The presence of NPHG could be expained by Pappus' chain theorem.)

Proof

From the proof of Lemma 6 is it obvious that the two quadrilaterals in question are rectangles. What needs to be shown is that each has equal sides.

Squares In Arbelos, auxiliary lnes

For the rectangle NPHG, as was observed by Mariano Perez de la Cruz, the result follows from a more general property known yet to Pappus: for a sequence of circles tangent to its neighbors and to two tangent semicircles with common center line, h_n = 2nR_n, where, for the circle #n in the sequence, R_n is the radius and h_n is the distance from its center to the common base center line. In our diagram GH serves as the diameter of the circle #1 in such a sequence, with h_n = 2R_n, GH = 2R_n, and GN = h_n.

For the rectangle CKDI, the proof is more involved. To start off, note a sequence of intersecting circumcircles of cyclic quadrilaterals: BKMP, KHFM, EFHG, EGIL, ANLI. Apply the Intersecting Secants Theorem to point C and the circles

(1)

CP·BC = CM·CK = CF·CH = CE·CG = CL·CI = CN·AC.

Next, let's recollect another result from the proof of Lemma 6

(2)

AN / NP = NP / BP.

We are going to use this shortly. But before we do, consider two pairs of similar triangles: ANL, HGL and BPM, GHM, from which we derive

(3)

AN / GH = LN / GL, and BP / GH = MP / HM.

Since GH = NP, and using (2), we see that

(4)

HM / MP = NP / BP = AN / NP = LN / GL,

from which

(5)

HM / MP + 1 = LN / GL + 1, or HP / MP = GN / GL

implying MP = GL and subsequently HM = LN.

Generally, the circle with diameter LM cuts each of the sides of square NPHG in two points. C is one such point on side NP. The eight points are split into two groups of vertices of two squares as in one of the proofs of the Pythagorean theorem, Proof 4 or Proof 9, with all cutoff triangles equal. In particular, ΔCLN = ΔCMP

(6)

CL = CM.

But from (1), CM·CK = CL·CI making CK = CI, which proves that CKDI is also a square.

The diagram has many other interesting properties. For example,

CP / CN = AC / BC

follows from (1). But, as was observed by Greg Markowsky, there are more proportions:

AC / BC = LN / GL = CP / CN = HM / MP = AD / BD = AI / CI = CK / BK.

There are also more circles and more incidences:

Squares In Arbelos, auxiliary everythings

71931984