This proof is one of the earliest. It has been appreciatively popularized by Coxeter and Greitzer. Morley's theorem was presented as a problem in Mathematical Questions and Their Solutions sections in the Educational Times (New Series), v 15 (1909), p. 47. One of the solutions sent in was by M. T. Naraniengar and is discussed below.

Naraniengar's proof depends on the following

Lemma

If four points Y', Z, Y, Z' satisfy the conditions

1. Y'Z = ZY = YZ' and
2. ∠YZY' = ∠Z'YZ = 180° - 2a > 60°

then they lie on a circle. Moreover, if a point A, on the side of the line Y'Z' away from point Y, is so situated that ∠Y'AZ' = 3a, then this fifth point A also lies on the same circle.

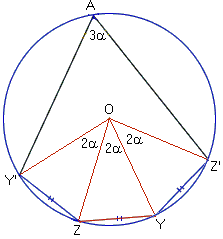
Following Coxeter and Greitzer, let the bisectors of angles YZY' and Z'YZ meet at O. Then triangles OY'Z, OZY, OYZ' are congruent and isosceles having base angles 90° - a. Their equal sides OY', OZ, OY, and OX' are radii of a circle with center O, and their angles at vertex O are all equal 2a. In other words, each of the equal chords Y'Z, ZY, YZ' subtends a central angle 2a and consequently subtends an angle a at any point on the arc Y'Z' not containing Y. This arc is the locus of points (on the side of the line Y'Z' away from Y) from which the chord Y'Z' subtends an angle 3a. One such point is A; therefore A lies on the circle.

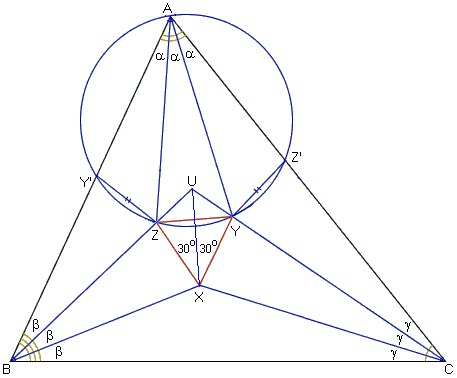
Now for the proof of Morley's theorem. Morley's trisectors of angles B = 3b and C = 3g meet in points U and X as in the diagram. In ΔBCU angles B and C are bisected by BX and CX; hence X is the incenter of the triangle and UX is the bisector of the angle at U. Construct points Y and Z on BU and CU such that

Then triangles ZXU and YXU are equal by ASA. Therefore, XY = XZ and ΔXYZ is equilateral.

In addition, ΔUZY is isosceles with base angles at Y and Z equal to b + g. Let also the angle at be 3a, then a + b + g = 60° and b + g = 60° - a. Thus,

Next, mark Y' on AB and Z' on AC so that

This makes triangles BZX and BZY' congruent by SAS; and the same holds for triangles CYX and CYZ'. Thus we make a step towards the premises of Lemma:

We have to check the second condition:

Similarly, ∠Z'YZ = 180° - 2a; and of course a = A/3 < 60°. By Lemma, the five points Y', Z, Y, Z', A lie on a circle. Since the equal chords Z'Y, YZ, ZY' subtend equal angles a at A, the lines AZ and AY trisect the angle A of ΔABC. In other words, the points X, Y, Z that were artificially constructed so as to form an equilateral triangle, are in fact the points of intersection of Morley's trisectors. Q.E.D.

References

1. H. S. M. Coxeter, S. L. Greitzer, Geometry Revisited, MAA, 1967

Morley's Miracle

1. J.Conway's proof
   • Remarks on J. Conway's proof
2. D. J. Newman's proof
3. Bankoff's proof
4. B. Bollobás' proof
5. Another proof
6. Nikos Dergiades' proof
7. G. Zsolt Kiss' proof
8. M. T. Naraniengar's proof
9. Doodling and Miracles
10. Morley's Pursuit of Incidence
11. Lines, Circles and Beyond
12. On Motivation and Understanding
13. Bankoff's conundrum
14. Of Looking and Seeing
15. Morley's Redux and More, Alain Connes' proof
16. An Unexpected Variant
17. Proof by B. Stonebridge and B. Millar
18. Proof by B. Stonebridge
19. Proof by Nolan L Aljaddou
20. Proof by Roger Smyth
21. Proof by H. D. Grossman
22. Proof by R. J. Webster
23. Proof by H. Shutrick

|Contact| |Front page| |Contents| |Geometry| |Store|

Copyright © 1996-2012 Alexander Bogomolny