Two Conditions for a Triangle to Be Equilateral

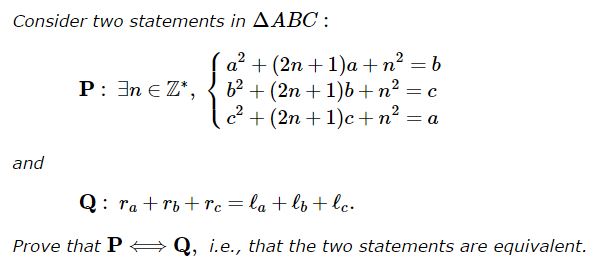
(The problem uses notations common in triangle geometry.)

Note that the proofs below in fact show more, viz., that both conditions only hold for equilateral triangles, which makes them automatically equivalent.

Adding up the three equations in $\mathbf{P},\;$

$\displaystyle\sum_{cycl}a^2+(2n+1)\sum_{cycl}a+3n^2=\sum_{cycl}a,$

i.e.,

$\displaystyle\sum_{cycl}a^2+2n\sum_{cycl}a+3n^2=0,$

which we rewrite as

$\displaystyle 3n^2+\left(2\sum_{cycl}a\right)n+\sum_{cycl}a^2=0.$

Since, it is given that the equation has a solution in integers, hence in reals, the discriminant $\Delta\;$ of this quadratic (in $n)\;$ equation is not negative

$\displaystyle\Delta =4\left(\sum_{cycl}a\right)^2-12\sum_{cycl}a^2\ge 0.$

This is equivalent to

$\displaystyle\sum_{cycl}a^2+2\sum_{cycl}ab-3\sum_{cycl}a^2\ge 0,$

which reduces to $\displaystyle\sum_{cycl}ab\ge\displaystyle\sum_{cycl}a^2,\;$ but, by say, the Rearrangement inequality, we have $\displaystyle\sum_{cycl}ab\le\displaystyle\sum_{cycl}a^2,\;$ implying that $\displaystyle\sum_{cycl}ab = \displaystyle\sum_{cycl}a^2.\;$ From here $\displaystyle\sum_{cycl}(a-b)^2=0,\;$ so that $a=b=c.$

For $\mathbf{Q},\;$ we have

$\displaystyle\sum_{cycl}r_a=4R+r\ge\sum_{cycl}m_a\ge\sum_{cycl}\ell_a,$

with equality only when $a=b=c.$

For any $n\in\mathbb{Z}^{*},\;$ the graph of the function $y=f(x)=x^2+(2n+1)x+n^2\;$ is tangent to the diagonal $y=x\;$ for $x=-n,\;$ otherwise being above the diagonal.

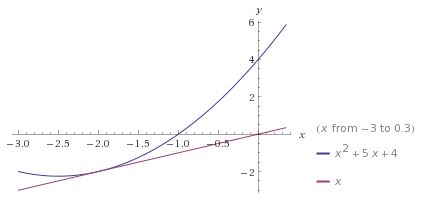
Iterations $x_{k+1}=f(x_k)\;$ converge to the point of tangency, never forming a $3-\mbox{loop}.\;$ It follows, therefore, from the definition of $\mathbf{P}\;$ that it may only hold when $a=b=c.$

Concerning $\mathbf{Q},\;$ with $2p=a+b+c,\;$ we have, say, by the AM-GM inequality,

$\displaystyle\ell_a=\sqrt{p(p-a)}\frac{2\sqrt{bc}}{b+c}\le\sqrt{p(p-a)}=\frac{S}{\sqrt{(p-b)(p-c)}},$

by Heron's formula. (The equality is only for $b=c.)\;$ On the other hand, say $\displaystyle r_a=\frac{S}{p-a}.\;$ Thus,

$\displaystyle\ell_a\le\frac{S}{\sqrt{(p-b)(p-c)}}=\sqrt{r_br_c}.$

But then, by the Cauchy-Schwarz inequality, we get

$\displaystyle\sum_{cycl}\ell_a\le\sum_{cycl}\sqrt{r_br_c}\le r_a+r_b+r_c,$

where the first inequality becomes equality only for $a=b=c\;$ while the second is the equality only for $r_a=r_b=r_c,\;$ which is the same.

The above problem from the Romanian Mathematical Magazine and a solution (Solution 1 by Soumava Chakraborty, Kolkata, India) has been kindly posted at the CutTheKnotMath facebook page by Dan Sitaru.