Graphing Equations Is Useful, III

Here is one problem suggested by Bulgaria for the 1967 International Mathematical Olympiad [Compendium, p.42]:

Solve the system:

\( \begin{array}{3,2} x^{2}+x-1=y \\ y^{2}+y-1=z \\ z^{2}+z-1=x. \end{array} \)

Solution

References

D. Djukic et al, The IMO Compendium, Springer, 2011 (Second edition)

Solve the system:

\( \begin{array}{3,2} x^{2}+x-1=y \\ y^{2}+y-1=z \\ z^{2}+z-1=x. \end{array} \)

The system is naturally related to the question of existence of either fixed points or cycles for the iterations (discrete dynamic system) defined by function \(f(x)=x^{2}+x-1\). Elsewhere we considered the system defined by the function \(\displaystyle f(x)=\frac{2x^{2}}{1+x^{2}}\) and by the function \(f(x)=1-x^{2}\). There is also a more general problem that was offered at the 1968 IMO. In all cases it is useful to visualize the graphs of \(y=f(x)\) and \(y=x\), for this is a convenient way to see a solution at a glance

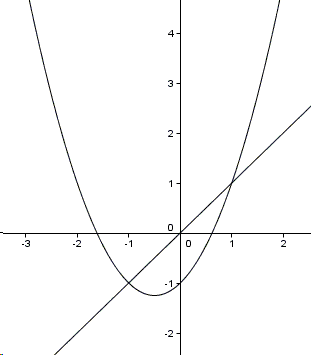
graph of the function y= x^2+x-1

It is immediate from the diagram (and is easily verified algebraically) that the equation \(f(x)=x\) has two solutions: \(x=\pm 1\). Accordingly, the given system has two solutions \((1,1,1)\) and \((-1,-1,-1)\). The task is to establish that there are no other solutions. (Note in passing that the very same consideration will apply to a similar system with more than three equations.)

It helps to observe that \(x=1\) is a repelling, while \(x=-1\) is an attractive, fixed points. In part, the iterations that start with \(x\gt 1\) produce an increasing sequence, for then \(x^{2}+x-1\gt x\). As an implication for the given system,

\(x \lt f(x) = y \lt f(y) = z \lt f(z) = x\)

shows that the system may not have a solution in which one of the variables exceeds \(1\).

It is also true that no solution may have one of the variables below \(-2\), because \(x\lt -2\) implies \(f(x)\gt 1\).

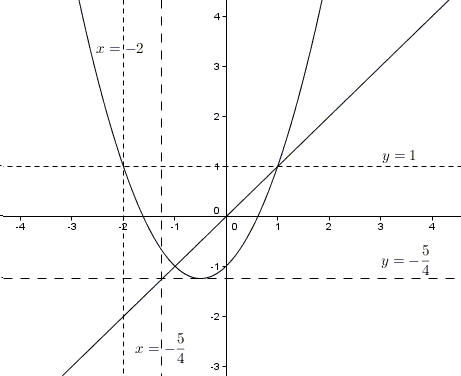
graph of the function y= x^2+x-1 and extra info

On the other hand, \(t\gt f(t)\), for \(t\in(-1,1)\), such that \(-1\lt x, y, z\lt 1\) leads to a contradiction:

\(x \gt f(x) = y \gt f(y) = z \gt f(z) = x\)

So, for the last step, assume that one of them, say \(x\), is less than \(-1\): \(x\in(-2,-1)\). What then?

First, if \(x\) is part of a solution, then \(x=f(z)\ge -\frac{5}{4}\), which is the minimum of \(f\). We thus can restrict \(x\) further and assume that \(x\in[-\frac{5}{4},-1)\). But this requires \(z\in (-1,0)\) and also implies \(y\in (-1,0)\). But this is a contradiction, because, for \(y\in (-1,0)\), \(z=f(y)\in [-\frac{5}{4},-1)\) and \([-\frac{5}{4},-1)\cap (-1,0)=\emptyset\).

Thus the only remaining possibilities are \(x=y=z=1\) and \(x=y=z=-1\).

Systems of Iterated Equations

71536896